Benutzer:Schnirch

Die Kukulkan-Pyramide in Chichén Itzá (Mexiko). Erbaut von den Mayas. Wer so was bauen kann, muss sich in Geometrie auskennen!


Volumen V einer Pyramide der Höhe h und der Schnittfläche 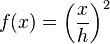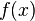$f(x) =\left( \frac{x}{h}\right) ^{2}$$f(x)$ einer Ebene F, die parallel zur Grundfläche A der Pyramide im Abstand x zur Spitze der Pyramide steht: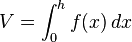 $V=\int_{0}^{h} f (x)\,dx$
Da die Schnittfläche 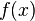$f(x)$ an der Stelle x durch eine zentrische Streckung der Grundfläche A mit dem Faktor 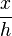$\frac{x}{h}$ entsteht, ist also 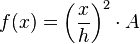$f(x) =\left( \frac{x}{h}\right) ^{2}\cdot A$ und damit:
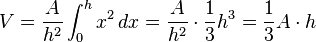$V=\frac{A}{h^{2}}\int_{0}^{h} x^{2}\,dx= \frac{A}{h^{2}}\cdot\frac{1}{3}h^{3}=\frac{1}{3}A\cdot h$.