Lösung von Aufgabe 12.02 WS 12 13
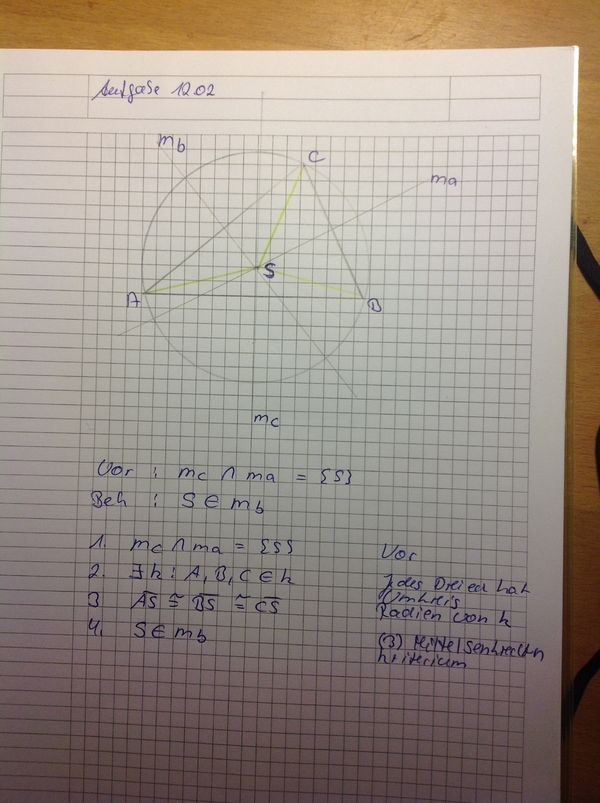
Aufgabe 12.02Beweisen Sie: Die Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt.
Lösung User ...
Lösung User Caro44--Caro44 13:16, 30. Jan. 2013 (CET) |
Frage Hauler
Stimmen mit Lösung von Caro44 überein. Frage die aufkam:
Wann nimmt man die Definition, wann nimmt man die Existenz und Eindeutigkeit ( in diesem Fall Mittelpunkt, Mittelsenkrechte), wann nimmt das Kriterium als Begründung?
Gedanken von uns: Im Beweis benutzen wir Definition nur, wenn Existenz und Eindeutigkeit bewiesen wurde. Kann man sich somit Existenz und Eindeutigkeit sparen und immer Definition schreiben? Weiter folgend kam diese Frage auch bei Definition oder Kriterium Mittelsenkrecht auf. Kriterium setzt sich ja aus beiden Definitionen zusammen!
--Hauleri 15:32, 30. Jan. 2013 (CET)