13)

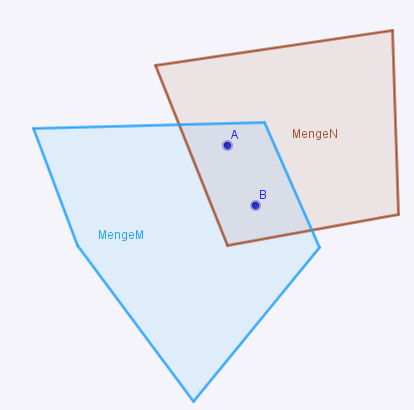
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.

Voraussetzung	M und N sind konvex--Der Bohrer 14:08, 13. Dez. 2012 (CET)
Behauptung	Schnittmenge ist konvex--Der Bohrer 14:08, 13. Dez. 2012 (CET)

Beweisschritt	Begründung
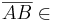1 A $\in$ M, B $\in$ M $\Rightarrow$ $\overline{AB} \in$ M	Weil M konvex ist
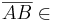2 A $\in$ N, B $\in$ N $\Rightarrow$ $\overline{AB} \in$ N	Weil N konvex ist
3 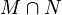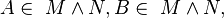$\ M \cap N$ $\Rightarrow$ $A \in \ M \wedge N, B \in \ M \wedge N,$	1), 2)
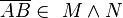4 $\overline{AB} \in \ M \wedge N$	3)

Weil $\overline{AB}$ Element der Schnittmenge ist. Ist die Schnittmenge konvex. Somit ist die Behauptung korrekt.

Geht das mit dem und Zeichen oder muss ich das für jede Menge extra machen? --Würmli 13:09, 4. Feb. 2013 (CET)

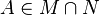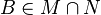Würmli, dein Bewei enthält einige richtige Schritte. Das Problem ist allerdings, dass der Ansatz so nicht stimmt. Du kannst nicht zwei Punkte aus in der Menge A wählen und später (Schritt 2 ) behaupten, dass sie auch in B liegen. Um den Beweis richtig zu führen, musst du A und B so wählen, dass gilt: $A \in M \cap N$ und $B \in M \cap N$ . Anschließend kannst du Schritt 1 und 2 daraus ableiten.--Tutorin Anne 16:02, 5. Feb. 2013 (CET)

Navigationsmenü