Implikationen
Beispiele
Beispiel 1
50px
Wenn der BVB im Finale der Champions League das erste Tor des Spieles schießt, dann gewinnt er die Champions League der Saison 2012/13.
Beispiel 2
Wenn ein Trapez ein Rechteck ist, dann sind sein Diagonalen kongruent zueinander.
Beispiel 3
Wenn ein Boxer während des Kampfes seinem Gegner den Rücken zukehrt, hat er den Kampf verloren.
Beispiel 4
Wenn zwei Winkel Stufenwinkel an geschnittenen Parallelen sind, dann sind sie kongruent zueinander.
Grundlegender Aufbau
- Wenn Bedingung
 , dann Behauptung , dann Behauptung  . .
- Aus
 folgt folgt  . .
-

Zusammenhang zur hinreichenden Bedingung
Ist die Aussage  wahr, so ist die Bedingung der Implikation hinreichend dafür, dass die Behauptung b gilt. wahr, so ist die Bedingung der Implikation hinreichend dafür, dass die Behauptung b gilt.
"Versteckte" Implikationen
Beispiele
Beispiel 1: Stufenwinkelsatz
Ohne Wenn-Dann
- Stufenwinkel an geschnittenen Parallelen sind kongruent zueinander
Wenn-Dann-Form
- Wenn zwei Winkel Stufenwinkel an geschnittenen Parallelen sind, dann sind sie kongruent zueinander.
Voraussetzung
- die beiden Winkel sind Stufenwinkel
- an geschnittenen Parallelen
Behauptung
- die beiden Winkel sind kongruent zueinander
Beispiel 2: Innenwinkelsatz für Dreiecke
Ohne Wenn-Dann
- In jedem Dreieck beträgt die Summe der Größen seiner Innenwinkel
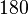 °. °.
Wenn-Dann-Form
- Wenn ein n-Eck ein Dreieck ist, dann beträgt die Summe der Größen seiner Innenwinkel
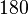 °. °.
Voraussetzung
- Das betrachtetet n-Eck ist ein Dreieck
Behauptung
- Die Summe der Größen seiner Innenwinkel beträgt
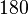 °. °.
Beispiel 3: Umkehrung des Thalessatzes
Ohne Wenn-Dann
- Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der längsten Seite dieses Dreiecks.
Wenn-Dann-Form
- Wenn ein Dreieck rechtwinklig ist, dann liegt der Mittelpunkt seines Umkreises auf der längsten seiner Seiten.
Voraussetzung
- Das betrachtete Dreieck ist rechtwinklig.
Behauptung
- Der Mittelpunkt seines Umkreises liegt auf der längsten seiner Seiten.
Implikationen als mathematische Sätze
mathematische Sätze
- Unter einem mathematischen Satz (im folgenden kurz Satz) versteht man eine mathematische Aussage, die wahr ist.
Implikationen als Sätze
- In der Regel werden Sätze als Implikationen formuliert.
- Die Voraussetzung der Implikation ist dann eine hinreichende Bedingung für die Behauptung der Implikation.
Die Implikation einer Behauptung und die Implikation als Behauptung (umgangssprachlich)
- Der Begriff der Behauptung wird natürlich auch umgangssprachlich verwendet. Meine Erfahrung lehrt mich, dass Novizen der mathematischen Logik diesbezüglich zu Verwechslungen neigen:
Eine gewagte Behauptung
- Wenn der FC Barcelona ohne Messi spielt, dann halbiert sich seine Spielstärke.
- Fans des FC Barcelona werden die gesamte Implikation (also die gesamte Aussage Wenn der FC Barcelona ohne Messi spielt, dann halbiert sich seine Spielstärke.) als eine gewagte Behauptung ansehen.
- Demgegenüber ist die Aussage Barcelona spielt ohne Messi die Voraussetzung der Implikation und die Aussage die Spielstärke halbiert sich die Behauptung der Implikation.
Notwendigkeit des Beweises eines Satzes
- Obige Implikation hinsichtlich der spielerischen Stärke des FC Barcelona in Anhängigkeit der Verfügbarkeit des Weltfußballers Messi wird nur schwer zu beweisen sein und kann damit nicht als Satz im mathematischen Sinne verstanden werden. Mathematische Sätze sind wahre Aussagen und als solche zu beweisen.
Beweisbeispiele
Beispiel 1: Der Scheitelwinkelsatz
Vorab
Es sei bereits klar, dass Nebenwinkel supplementär sind (sich zu 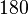 ° ergänzen). ° ergänzen).
Natürlich seien die Begriffe Scheitelwinkel und Nebenwinkel sauber definiert.
Der Satz
- Satz: (Scheitelwinkelsatz)
- Wenn zwei Winkel
 und und  Scheitelwinkel sind, so haben sie dieselbe Größe. Scheitelwinkel sind, so haben sie dieselbe Größe.
Der Beweis

|
 , dann Behauptung
, dann Behauptung  .
.

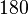 °.
°.
 und
und  Scheitelwinkel sind, so haben sie dieselbe Größe.
Scheitelwinkel sind, so haben sie dieselbe Größe.


