Aufgabe 12.04
Die Gerade  sei Tangente an den Kreis sei Tangente an den Kreis  (Mittelpunkt (Mittelpunkt  ) im Punkt ) im Punkt  . Beweisen Sie: . Beweisen Sie: 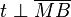 . .
Lösung
Annahme:
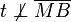 . .
Nach der Existenz des Lotes von  auf auf  muss es jetzt eine Strecke muss es jetzt eine Strecke 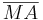 geben, die das Lot von geben, die das Lot von  auf auf  ist. Selbstverständlich ist ist. Selbstverständlich ist  verschieden von verschieden von  , da ansonsten , da ansonsten 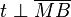 gelten würde. Weil gelten würde. Weil  Tangente an Tangente an  ist, kann ist, kann  nicht zu nicht zu  gehören. gehören.
Fall 1:
 liegt außerhalb von liegt außerhalb von  . Der Abstand von . Der Abstand von  zu zu  ist nun größer als der Radius ist nun größer als der Radius 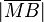 . .  liegt jedoch in liegt jedoch in 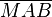 dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von 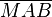 sein. sein.
Fall 2:
-
 liegt innerhalb von liegt innerhalb von  . Wir tragen auf . Wir tragen auf  die Länge die Länge 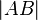 ab und erhalten auf ab und erhalten auf  den Punkt den Punkt 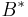 . Wegen Fehler beim Parsen(Syntaxfehler): \overline{AB\ \tilde= \overline{Ab^*} . Wegen Fehler beim Parsen(Syntaxfehler): \overline{AB\ \tilde= \overline{Ab^*}
und 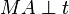 ist ist 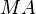 die Mittelsenkrechte von die Mittelsenkrechte von 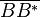 . Wegen des Mittelsenkrechtenkriteriums muss jetzt . Wegen des Mittelsenkrechtenkriteriums muss jetzt 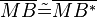 sein. Da nun sein. Da nun  ein Radius von ein Radius von  ist, muss auch ist, muss auch 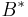 zu zu  gehören. Damit hätte gehören. Damit hätte  zwei verschiedene Punkte mit zwei verschiedene Punkte mit  gemeinsam, was im Widerspruch dazu steht, dass gemeinsam, was im Widerspruch dazu steht, dass  Tangente an Tangente an  ist. ist.
Zurück zu: Serie 12 SoSe 2013
|  sei Tangente an den Kreis
sei Tangente an den Kreis  (Mittelpunkt
(Mittelpunkt  ) im Punkt
) im Punkt  . Beweisen Sie:
. Beweisen Sie: 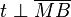 .
.
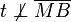 .
.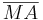 geben, die das Lot von
geben, die das Lot von  verschieden von
verschieden von 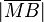 .
.  liegt jedoch in
liegt jedoch in 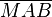 dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von
dem rechten Winkel gegenüber und muss demzufolge die längst der Seiten von  die Länge
die Länge 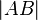 ab und erhalten auf
ab und erhalten auf 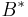 . Wegen Fehler beim Parsen(Syntaxfehler): \overline{AB\ \tilde= \overline{Ab^*}
. Wegen Fehler beim Parsen(Syntaxfehler): \overline{AB\ \tilde= \overline{Ab^*}
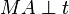 ist
ist 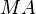 die Mittelsenkrechte von
die Mittelsenkrechte von 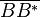 . Wegen des Mittelsenkrechtenkriteriums muss jetzt
. Wegen des Mittelsenkrechtenkriteriums muss jetzt 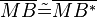 sein. Da nun
sein. Da nun 
