15)
a) Geben Sie die Menge  aller konvexer Drachenvierecke an.
aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge  .
.
c) Wir definineren eine Relation  mit
mit 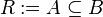 . Bestimmen Sie die Relation
. Bestimmen Sie die Relation  auf
auf  .
.
d) Untersuchen Sie die Relation  auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
zu a) M = {s.D., D, P, Ra, Re, Q}
die schiefen Drachen müssen hier nicht mit rein genommen werden --Schnirch (Diskussion) 14:22, 19. Nov. 2014 (CET)
Mit schiefen Drachen (plural) sind ja wohl sD, P und Re gemeint? --EarlHickey (Diskussion) 12:26, 9. Feb. 2015 (CET)
zu b) M x M = { (D,D), (D,Ra), (D,Q), (Ra,D), (Ra,Ra), (Ra,Q), (Q,D), (Q,Ra), (Q,Q)}
zu c) Die Relation R angewendet auf M x M, habe ich in Aufgabe b) dick markiert.
zu d) Die Relation ist reflexiv und transitiv, aber nicht symmetrisch (z.B.: Ra ist Teilmenge von D, aber D nicht Teilmenge von Ra).--Bienes (Diskussion) 13:12, 21. Nov. 2014 (CET)

