15)

Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:

$\overline{AB}\cap g=\lbrace \rbrace \wedge \overline{BC}\cap g=\lbrace \rbrace\Rightarrow \overline{AC}\cap g=\lbrace \rbrace$

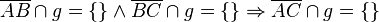
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 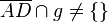$\overline{AD}\cap g\not=\lbrace \rbrace$ und nutzen Sie den Satz von Pasch)

 So  vielleicht?  

6.3 Lösung ?

Bei Schritt I, sollte als Begründung nicht der Begriff "Annahme" stehen. Dieser Begriff ist reserviert für einen indirekten Beweis
und bezeichnet immer die Verneinung der Behauptung. Sonst ist der Beweis in Ordnung!--Schnirch (Diskussion) 13:07, 19. Jan. 2015 (CET)