Der schwache Außenwinkelsatz
Inhaltsverzeichnis |
schwacher Außenwinkelsatz?
In der Vorlesung wurde angedeutet, dass es im Rahmen der absoluten Geometrie nicht möglich ist, den Satz über die Summe der Größen der Innenwinkel eines Dreiecks zu beweisen. Wenn es richtig ist, was in der Vorlesung gesagt wurde, dann dürfte es in der absoluten Geometrie auch nicht möglich sein, den sogenannten starken Außenwinkelsatz zu beweisen. Die folgende Applikation demonstriert den starken Außenwinkelsatz:
Egal, wie wir unser Dreieck  wählen, es gilt immer
wählen, es gilt immer 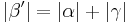 .
.
Allgemeiner formuliert:
Für jedes Dreieck gilt: Die Größe eines jeden Außenwinkels ist immer gleich der Summe der Größen der beiden Innenwinkel des Dreiecks, die zu dem jeweiligen Außenwinkel keine Nebenwinkel sind.
Wie bereits erwähnt, gilt der starke Außenwinkelsatz im Rahmen der absoluten Geometrie nicht. Es gilt jedoch der sogenannte schwache Außenwinkelsatz. Dieser ist selbstverständlich im starken Außenwinkelsatz aufgehoben.
Satz VIII.1: (schwacher Außenwinkelsatz)
- Die Größe eines jeden Außenwinkels eines Dreiecks ist jeweils größer als die Größe eines jeden Innenwinkels dieses Dreiecks, der kein Nebenwinkel zu dem gewählten Außenwinkel des Dreiecks ist.
Für den Beweis des schwachen Außenwinkelsatzes formulieren wir zunächst ein Lemma.
Lemma 2
- Wenn ein Punkt
 im Inneren des Winkels
im Inneren des Winkels  liegt, dann liegt der gesamte Strahl
liegt, dann liegt der gesamte Strahl 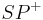 im Inneren des Winkels
im Inneren des Winkels  .
.
- Wenn ein Punkt
Hinsichtlich des Beweises von Lemma 2 verweisen wir auf das alte Skript (Geschichten aus dem Inneren).
Beweis von Satz VIII.1
Hilfskonstruktion
--Heinzvaneugen 10:12, 8. Jul. 2010 (UTC)
Danke --*m.g.* 19:37, 8. Jul. 2010 (UTC)
--Vankman 20:38, 8. Jul. 2010 (UTC)Sollte da nicht bei Schritt 2 CM = MP stehen??
Der letztendliche Beweis
Es bleibt zu zeigen: 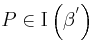 , wobei wir in diesem Fall das offene Innere von
, wobei wir in diesem Fall das offene Innere von 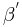 meinen.
meinen.
Das offene Innere von 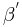 ist der Schnitt zweier offener Halbebenen
ist der Schnitt zweier offener Halbebenen  .
.
Der Punkt  würde gerade dann nicht im Inneren des Winkels
würde gerade dann nicht im Inneren des Winkels 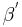 liegen,wenn er
liegen,wenn er
- in Halbenbene
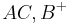
oder
- in der Halbebene
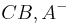
liegen würde.
zu 1.
Als Punkt der Halberaden 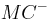 (Konstruktion von
(Konstruktion von  ) kann
) kann  nicht mit
nicht mit  auf ein und derselben Seite bezüglich
auf ein und derselben Seite bezüglich  liegen.
liegen.
zu 2.
2.a
Annahme: 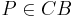 In diesem Fall würde gelten:
In diesem Fall würde gelten: 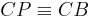 . (Begründung mittels Inzidenzaxiomen ist jetzt nicht mehr nötig.) Wir wollen uns darauf einigen die Gerade
. (Begründung mittels Inzidenzaxiomen ist jetzt nicht mehr nötig.) Wir wollen uns darauf einigen die Gerade  mit
mit  zu bezeichnen.
zu bezeichnen.
Die Gerade 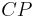 hat mit der Geraden
hat mit der Geraden  genau einen Punkt gemeinsam, den Punkt
genau einen Punkt gemeinsam, den Punkt  .
.
Die Gerade 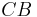 hat mit der Geraden
hat mit der Geraden  genau einen Punkt gemeinsam, den Punkt
genau einen Punkt gemeinsam, den Punkt  .
.
Da die beiden Geraden 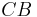 und
und 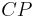 identisch sind und die nichtidentischen Geraden
identisch sind und die nichtidentischen Geraden  und
und  maximal einen Punkt gemeinsam haben können,
maximal einen Punkt gemeinsam haben können,
müssen die beiden Punkte  und
und  identisch sein.
identisch sein.
Letzteres ist ein Widerspruch zur Wahl von  .
. ist nämlich der Mittelpunkt von
ist nämlich der Mittelpunkt von  .
.
2.b
Annahme: 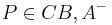
Nach der Konstruktion des Punktes  als Punkt der Halbgeraden
als Punkt der Halbgeraden 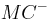 ist
ist  ein Punkt der Strecke
ein Punkt der Strecke 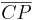 .
.
Die Halbebene 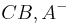 ist eine konvexe Punktmenge.
ist eine konvexe Punktmenge.
Als Punkt der Trägergeraden 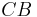 gehört
gehört  zur Halbeben
zur Halbeben 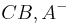 .
.
Der Punkt  gehört nach unserer Annahme zur Halbebene
gehört nach unserer Annahme zur Halbebene 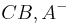 .
.
Wegen der Konvexität von 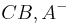 gehört die gesamte Strecke
gehört die gesamte Strecke 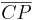 zur Halbebene
zur Halbebene 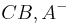 und damit natürlich auch der Punkt
und damit natürlich auch der Punkt  .
.
Letzteres bedeutet, dass  und
und  in verschiedenen Halbebene bezüglich
in verschiedenen Halbebene bezüglich 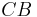 liegen.
liegen.
Dieses impliziert, dass die Stecke 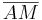 durch die Gerade
durch die Gerade 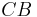 geschnitten wird.
geschnitten wird.
Der einzige gemeinsame Schnittpunkt der Geraden 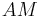 und
und 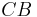 ist der Punkt
ist der Punkt  .
.
Weil  ein Punkt der Strecke
ein Punkt der Strecke 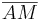 wäre, könnte
wäre, könnte  nicht gleichzeitig der Mittelpunkt von
nicht gleichzeitig der Mittelpunkt von  sein.
sein.
Überprüfen Sie Ihr Verständnis: Ist Schritt 2.a wirklich nötig? Wenn ja warum?

