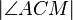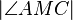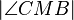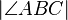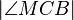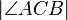Lösung von Aufgabe 3.07 SoSe 2017 S
Aus Geometrie-Wiki
Version vom 11. Mai 2017, 15:10 Uhr von Rosa Einhorn (Diskussion | Beiträge)
Aufgabe 3.07 SoSe 2017 SGegeben sei ein Dreieck Begründen Sie die Korrektheit Ihrer Berechnungen außschließlich unter Verwendung der folgenden Sätze:
Lösung 1
Lösung 2 |
 mit dem Umkreis
mit dem Umkreis  . Der Mittelpunkt von
. Der Mittelpunkt von  sein. Der Winkel
sein. Der Winkel 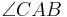 habe die Größe
habe die Größe 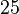 °. Berechnen Sie die folgenden Winkelgrößen:
°. Berechnen Sie die folgenden Winkelgrößen: