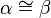Implikationen
Generelle Kennzeichnung von Implikationen
Implikationen sind spezielle mathematische Aussagen, deren Typ sich kurz als wie folgt darstellen bzw. beschreiben lässt:
- Wenn
 dann dann  . .
- Aus
 folgt folgt  . .
-
 impliziert impliziert  . .
-
 ist eine Folgerung aus ist eine Folgerung aus  . .
- Unter der Voraussetzung, dass
 gilt, gilt auch gilt, gilt auch  . .
-
 ist hinreichend dafür, dass ist hinreichend dafür, dass  gilt. gilt.
-

Die Aussage  heißt in der Implikation heißt in der Implikation  Voraussetzung, die Aussage Voraussetzung, die Aussage  wird Behauptung genannt. wird Behauptung genannt.
Beispiele
Implikation 1: Satz zur Teilbarkeit durch 3
- Wenn die Quersumme
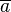 einer natürlichen Zahl einer natürlichen Zahl  durch durch  teilbar ist, dann ist auch die Zahl teilbar ist, dann ist auch die Zahl  durch durch  teilbar. teilbar.
- In Formelsprache:
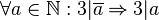
- Voraussetzung:
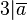
- Behauptung:
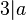
Implikation 2: Satz zur Teilbarkeit von Summen
- Für alle natürlichen Zahlen
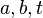 gilt: gilt:
- Wenn
 die Zahlen die Zahlen  und und  teilt, dann teilt teilt, dann teilt  auch die Summe auch die Summe 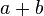 . .
- In Formelsprache:
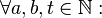
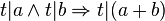
- Voraussetzung: Wir haben zwei Voraussetzungen die durch das logische und zu einer Voraussetzung zusammengefasst werden:
- V1:
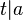
- V2:
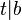
- V:
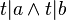
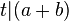
Implikation 3: Nebenwinkelsatz
- Wenn
 und und  Nebenwinkel sind, dann ist die Summe ihrer Größen Nebenwinkel sind, dann ist die Summe ihrer Größen 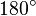
In anderer Formulierung ohne wenn-dann:
- Nebenwinkel ergänzen sich zu
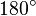
-
 und und  sind Nebenwinkel sind Nebenwinkel
 und und  sind supplementär. sind supplementär.
Implikation 4: Scheitelwinkelsatz
- Wenn die beiden Winkel
 und und  Scheitelwinkel sind, dann haben sie dieselbe Größe. Scheitelwinkel sind, dann haben sie dieselbe Größe.
alternative Formulierung ohne wenn-dann:
- Scheitelwinkel haben dieselbe Größe. oder
- Scheitelwinkel sind kongruent zueinander.
 und und  sind Scheitelwinkel sind Scheitelwinkel
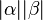 bzw. bzw. 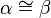
|
 dann
dann  .
.

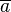 einer natürlichen Zahl
einer natürlichen Zahl  teilbar ist, dann ist auch die Zahl
teilbar ist, dann ist auch die Zahl 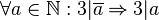
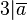
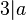
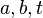 gilt:
gilt: die Zahlen
die Zahlen 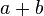 .
.
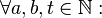
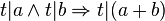
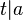
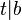
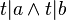
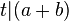
 und
und  Nebenwinkel sind, dann ist die Summe ihrer Größen
Nebenwinkel sind, dann ist die Summe ihrer Größen 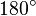
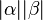 bzw.
bzw.