Aufgabe 3.1
Es seien 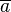 und und 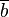 zwei Restklassen bzgl. des selben Moduls zwei Restklassen bzgl. des selben Moduls  . Beweisen Sie die Repräsentantenunabhängigkeit Restklassenaddition: . Beweisen Sie die Repräsentantenunabhängigkeit Restklassenaddition:
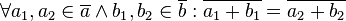 . .
Aufgabe 3.2
Auf der Menge aller Brüche 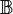 definieren wir deine Relation quotientengleich definieren wir deine Relation quotientengleich 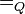 : :
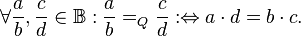
Zeigen Sie, dass 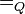 eine Äquivalenzrelation ist. eine Äquivalenzrelation ist.
Aufgabe 3.3
Die Relation quotientengleich 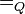 ist eine Äquivalenzrelation auf der Menge aller Brüche und zieht damit eine Klasseneinteilung nach sich. Die Menge aller Äquivalenzklassen nach ist eine Äquivalenzrelation auf der Menge aller Brüche und zieht damit eine Klasseneinteilung nach sich. Die Menge aller Äquivalenzklassen nach 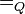 ist die Menge der gebrochenen Zahlen ist die Menge der gebrochenen Zahlen 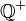 . Eine gebrochene Zahl . Eine gebrochene Zahl 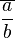 ist damit eine Äquivalenzklasse nach der Relation ist damit eine Äquivalenzklasse nach der Relation 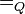 , d.h. der Bruch , d.h. der Bruch 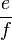 gehört genau dann zu gehört genau dann zu 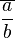 , wenn , wenn 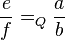 gilt. Beweisen Sie die Repräsentantenunabhängigkeit der Multiplikation gebrochener Zahlen. gilt. Beweisen Sie die Repräsentantenunabhängigkeit der Multiplikation gebrochener Zahlen.
Aufgabe 3.4
Aufgabe 3.5
Aufgabe 3.6
Aufgabe 3.7
Aufgabe 3.8
Aufgabe 3.9
Aufgabe 3.10
| 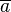 und
und 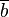 zwei Restklassen bzgl. des selben Moduls
zwei Restklassen bzgl. des selben Moduls  . Beweisen Sie die Repräsentantenunabhängigkeit Restklassenaddition:
. Beweisen Sie die Repräsentantenunabhängigkeit Restklassenaddition: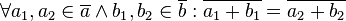 .
.
 definieren wir deine Relation quotientengleich
definieren wir deine Relation quotientengleich  :
: 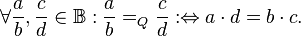
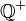 . Eine gebrochene Zahl
. Eine gebrochene Zahl 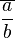 ist damit eine Äquivalenzklasse nach der Relation
ist damit eine Äquivalenzklasse nach der Relation 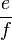 gehört genau dann zu
gehört genau dann zu 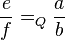 gilt. Beweisen Sie die Repräsentantenunabhängigkeit der Multiplikation gebrochener Zahlen.
gilt. Beweisen Sie die Repräsentantenunabhängigkeit der Multiplikation gebrochener Zahlen.

