Aufgabe 4.1
Wir betrachten auf der Menge der natürlichen Zahlen, die Relationen Teiler und echter Teiler.
(a) Eine dieser Relationen ist keine Äquivalenzrelationen. Welche? Beweisen Sie Ihre Aussage.
(b) Beweisen Sie für die andere Relation, dass sie eine Äquivalanzrelation ist.
Aufgabe 4.2
Die Gleichung 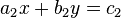 ist eine Linearkombination der Gleichung ist eine Linearkombination der Gleichung 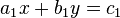 , wenn eine Zahl , wenn eine Zahl 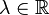 derart existiert,
dass derart existiert,
dass
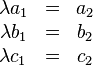
gilt.
(a) Beweisen Sie: Die Relation Gleichung b ist Linearkombination von Gleichung a ist eine Äquivalenzrelation auf der Menge der Gleichungen vom Typ  . .
(b) Interpretieren Sie die Relation geometrisch.
Aufgabe 4.3
Es sei 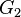 die Menge aller Gleichungen vom Typ die Menge aller Gleichungen vom Typ  . . 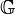 sei die Menge aller Äquivalenzklassen sei die Menge aller Äquivalenzklassen 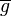 , in die , in die  durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf 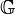 die folgende Operation die folgende Operation  : : 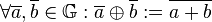 . Beweisen Sie: . Beweisen Sie: ![[\mathbb{G}, \oplus]](/images/math/f/9/7/f973823fb9e00ff432d68505910909a8.png) ist Gruppe. ist Gruppe.
Aufgabe 4.4
Aufgabe 4.5
Aufgabe 4.6
Aufgabe 4.7
Aufgabe 4.8
Aufgabe 4.9
Aufgabe 4.10
| 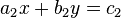 ist eine Linearkombination der Gleichung
ist eine Linearkombination der Gleichung 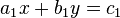 , wenn eine Zahl
, wenn eine Zahl 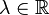 derart existiert,
dass
derart existiert,
dass 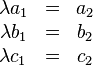
 .
.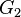 die Menge aller Gleichungen vom Typ
die Menge aller Gleichungen vom Typ 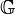 sei die Menge aller Äquivalenzklassen
sei die Menge aller Äquivalenzklassen 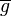 , in die
, in die  durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf
durch die Äquivalenzrelation Gleichung a ist Linearkombination von Gleichung b eingeteilt wird. Wir definieren auf  :
: 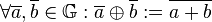 . Beweisen Sie:
. Beweisen Sie: ![[\mathbb{G}, \oplus]](/images/math/f/9/7/f973823fb9e00ff432d68505910909a8.png) ist Gruppe.
ist Gruppe.

