Lösung von Aufgabe 9.5P (SoSe 18)

m sei Mittelsenkrechte der Strecke $\overline{AB}$. Beweisen Sie durch Kontraposition: $\left| AP \right| =\left| BP \right|\Rightarrow P\in m$
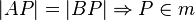
Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung.
Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.

Kontraposition: Strecke AP ist nicht = Strecke BP impliziert P ist nicht element von m
Voraussetzung:
Ein Punkt der auf der Gerade m liegt heißt D.
Es gibt einen Punkt C der in der Halbebene von A liegt und nicht m schneidet. Zudem ist die Strecke AC die längste und länger als AD.

Beweisschritt	Begründung
1) AD = BD und AD + BD = AB	Mittelsenkrechtenkriterium; Voraussetzung; Mathematische Gesetzte
2) D ist nicht gleich P	Kontraposition
3) AP ist nicht = BP impliziert AP >/< BP	1); 2)
4) AP und AC schneiden nicht M	Voraussetzung, 3)
5) Wenn AP und AC M nicht schneiden, dann schneidet PC M auch nicht.	Satz von Pasch; 4)
6) AC länger/gleich AP + AC & als AD	Voraussetzung; Dreiecksungleichung
7) AP < BP	5); 6)
8) P ist nicht Element von m	7), Mittelsenkrechtenkriterium

/goldxyz/