Lösung von Aufg. 6.4P (WS 18 19)

Aus Geometrie-Wiki
Version vom 23. November 2018, 13:05 Uhr von CIG UA (Diskussion | Beiträge)

(Unterschied) ← Nächstältere Version | Aktuelle Version (Unterschied) | Nächstjüngere Version → (Unterschied)
Wechseln zu: Navigation, Suche

a) Formulieren Sie die Kontraposition der Implikation aus Aufgabe 6.3.

Ist der Durchschnitt zweier Punktmengen konkav, dann sind entweder beide oder eine Punktmengen konkav.--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 19:26, 19. Nov. 2018 (CET)

Ist die Schnittmenge zweier Mengen nicht konvex, so ist mindestens eine der Mengen auch nicht konvex. --CIG UA (Diskussion) 13:05, 23. Nov. 2018 (CET)


b) Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 6.3 nicht wahr ist.

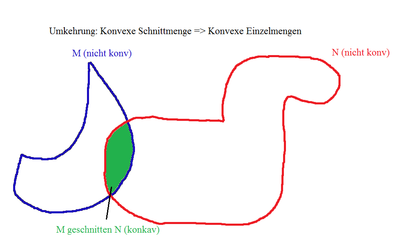Aufgabe 6 4 Schnittmengen.png--CIG UA (Diskussion) 13:05, 23. Nov. 2018 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._6.4P_(WS_18_19)&oldid=32554“