Lösung von Zusatzaufg.7.3P (WS 18 19)

Beweisen Sie: Das Innere eines Dreiecks ist konvex.

Das Innere eines Dreiecks ist die Schnittmenge von 3 Halbebenen: $\overline{ABC}$ = $\overline{AB}C^+$ ∩ $\overline{AC}B^+$ ∩ $\overline{BC}A^+$
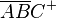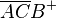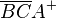
=> Halbebenen sind konvexe Mengen.
=> Das Innere eines Dreiecks ist eine Schnittmenge konvexer Mengen
=> Das Innere eines Dreiecks ist eine konvexe Menge. --CIG UA (Diskussion) 15:38, 30. Nov. 2018 (CET)

Für die letzte Aussage fehlt noch die Begründung--Schnirch (Diskussion) 13:09, 3. Dez. 2018 (CET)