19)
Aus Geometrie-Wiki
Version vom 11. Januar 2019, 21:07 Uhr von CIG UA (Diskussion | Beiträge)
Beweisen Sie Satz IX.2:
Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S, sowie zwei Punkten 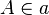 und
und 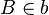 , die von S jeweils verschieden sind. Wir betrachten die Verkettung
, die von S jeweils verschieden sind. Wir betrachten die Verkettung  . Für einen beliebigen Punkt P und seinen Bildpunkt
. Für einen beliebigen Punkt P und seinen Bildpunkt  gilt:
gilt: 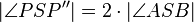 .
.
Vor: P"= Sa Sb(P). Beh: |<(PSP)|= 2|<(ASB)|
Sb(P). Beh: |<(PSP)|= 2|<(ASB)|
1.) Sa(P) = P' und Sb(P') = P" - Vor., Verkettung von Geradenspiegelung
2.) 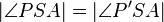 - 1.) Winkelmaßerhaltung
- 1.) Winkelmaßerhaltung
3.) 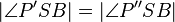 - 1.) Winkelmaßerhaltung
- 1.) Winkelmaßerhaltung
4.) 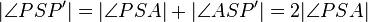 - 2.), Winkeladdition
- 2.), Winkeladdition
5.) 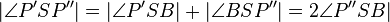 - 3.), Winkeladdition
- 3.), Winkeladdition
6.) 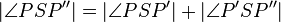 - Winkeladdition
- Winkeladdition
7.) 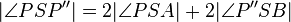 - 4.), 5.), 6.)
- 4.), 5.), 6.)
8.) 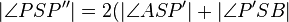 ) - 7.), Distributivgesetz
) - 7.), Distributivgesetz
9.) 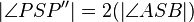 - 8.) Winkeladdition
- 8.) Winkeladdition
=> 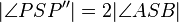 . Die Behauptung ist damit bewiesen.--CIG UA (Diskussion) 21:35, 20. Dez. 2018 (CET)
. Die Behauptung ist damit bewiesen.--CIG UA (Diskussion) 21:35, 20. Dez. 2018 (CET)

