19)

Beweisen Sie den Innenwinkelsatz für Dreiecke mit Hilfe zweier Punktspiegelungen.

Vor: $\overline{ABC}$ => |α| + |β| + |γ| = 180
1.) D_P1,180 (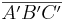$\overline{ABC}$) = $\overline{A'B'C'}$ mit P₁ ε a und |P₁C| = |P₁B| => C=B' und B=C' und a=a' - Def Drehung
2.) D_P2,180 (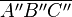$\overline{ABC}$) = $\overline{A''B''C''}$ mit P₂ ε b und |P₂C| = |P₂A| => C=A" und A=C" und b=b" - Def Drehung
3.) C, A', B" sind kollinear, da CA' = c' und CB = c => |α'| + |β"| + |γ| = 180 - 1.); 2.); Punktspiegelung von Geraden erzeugt parallele Geraden (deswegen kollinear)
4.) |α'| = |α| und |β"| = |β| - Winkelmaßerhaltung
5.) |α| + |β| + |γ| = 180 - 4.)
--CIG UA (Diskussion) 13:17, 25. Jan. 2019 (CET)