11
Inhaltsverzeichnis |
Beweise zu den Sätzen
Die Beweise auf dieser Seite sind aus dem Skript hier vom WIKI entnommen.
Beweis von Satz I.1
- Voraussetzung: Es seien g und h zwei Geraden, die nicht identisch sind.
- Fall 1:
- Die Geraden g und h haben keinen Punkt gemeinsam. In diesem Fall ist nichts weiter zu zeigen, denn sie haben damit nicht mehr als einen Punkt gemeinsam.
- Fall 2:
- Die Geraden g und h schneiden sich in einem Punkt P.
- Wir haben zu zeigen, dass sie keinen weiteren Punkt gemeinsam haben.
- Wir führen den Beweis indirekt und nehmen an, dass die Geraden g und h einen weiteren von P verschiedenen Punkt Q gemeinsam haben.
- Das Axiom I/1 sagt aus, dass durch zwei verschiedene Punkte genau eine Gerade geht. Da die beiden Punkte P und Q verschieden sind, kann auf sie dieses Axiom angewandt werden.
- Die Gerade g geht durch P und Q und die Gerade h geht durch P und Q. Da es nun eine und nur eine Gerade gibt, die durch P und Q geht, müssen die beiden Geraden g und h identisch sein.
- Das ist allerdings ein Widerspruch zur Voraussetzung, dass g und h nicht identisch sind.
Beweis von Satz I.2
- Es seien g und h zwei Geraden.
- Voraussetzung: g und h haben mehr als einen Punkt gemeinsam.
- Es seien dieses die Punkte P und Q.
- Wir haben zu zeigen, dass die beiden Geraden g und h identisch sind.
- Dieses folgt unmittelbar aus Axiom I/1.
- Die Annahme, dass ein weiterer gemeinsamer Punkt Q der beiden Geraden g und h existiert, ist damit zu verwerfen.
Dieser Beweis ist nicht schlüssig. Es wird von einer Annahme gesprochen, die nur aufgestellt wird, wenn es sich um einen indirekten Beweis handelt. Bei der Kontraposition wird direkt bewiesen.
Der weitere gemeinsame Punkt Q ist schon Element der Geraden g und h laut Voraussetung.
Also der Beweis wird wie folgt geführt.
Voraussetzung: g und h haben mehr als einen Punkt gemeinsam. P, Q sind Element der Geraden g und h
Behauptung: g und h sind identisch
1) P, Q sind Element von g und h____laut Voraussetzung
2) Durch die Punkte P und Q geht____Axiom I/1
genau eine Gerade.
3) g und h sind identisch__________2)
Behauptung stimmt q.e.d --Engel82 16:43, 15. Nov. 2010 (UTC)
Beweis von Satz I.3
Es existieren mindestents 3 paarweise verschiedene Geraden.
Voraussetzung: Geraden
Behauptung: die 3 Geraden g,h,l sind paarweise verschieden
Beweis:
(1) Es existiert eine Gerade g mit A Element g und B Element g_____________________ nach Voraussetzung, Axiom I.2
Es existiert eine Gerade h mit C Element h und D Element h
(2) nkoll(A,B,C____________________________________________________________________ nach (1), Axiom I.3
(3) zu zwei beliebig verschiedenen Punkten gibt es genau eine Gerade, die die
beiden Punkte enthält___________________________________________________________nach Axiom I.1
(4)AB, BC, AC_______________________________________________________________________nach (3)
noch zu zeigen: AB nicht identisch zu BC nicht identisch zu AC nicht identisch zu AB
Annahme: oBdA: AB=BC
Die Punkte A,B,C gehören ein und derselben Gerade an => koll(A,B,C)
Widerspruch zu Beweisschritt (2), Axiom I.3
=> die Annahme ist zu verwerfen, Behauptung stimmt
--Snoopy 1 14:10, 12. Dez. 2010 (UTC)
Beweis von Satz V.1
Hab mich mal an dem Beweis versucht, bin mir aber nicht sicher, ob man das so machen darf...
Satz: Das Innere eines Winkels ist konvex.
Voraussetzung: 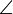 pSq , Punkt A und B
pSq , Punkt A und B  Inneres von
Inneres von 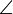 pSq
pSq
Behauptung: 
 Inneres von Winkel
Inneres von Winkel 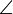 pSq
pSq
Beweis:
(1) Scheitel p des Winkels und Punkt A bilden die Halbebene 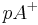
(Def. Halbebene, Vors.)
(2) Scheitel q des Winkels und Punkt B bilden die Halbebene 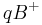
(Def.Halbebene, Vors.)
(3) B 
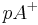
((1), Def. Inneres eines Winkels)
(4) A 
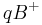
((2), Def. Inneres eines Winkels)
(5) 

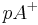
((1), (3), Axiom I.5)
(6) 

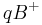
((2), (4), Axiom I.5)
(7) 

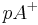
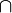
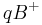
((5), (6))
(8)  ist konvex
ist konvex
((5), (6), (7), Satz IV.3)
(9) 
 Inneres von Winkel
Inneres von Winkel 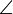 pSq
pSq
((8))
(10) Das Innere des Winkels 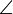 pSq ist konvex.
pSq ist konvex.
((9), Def. konvexe Punktmengen)
Lialin 18.36, 18. Jan. 2011 (UTC)