Diskussion:Lösung von Aufgabe 2.8 (SoSe 11)
Aus Geometrie-Wiki
Version vom 13. Juli 2011, 09:26 Uhr von *m.g.* (Diskussion | Beiträge)
Lösung von Celebino
Zeichne ein Dreieck mit den Strecken AB, BC und AC.
Entstanden ist das Dreieck ABC, mit den Winkeln BAC, ABC und ACB.
Wir betrachten nur den Winkel BAC.
Markiere die Hälfte der Strecke AB und der Strecke AC.
Es entstehen die Punkte N und M.
Verbinde nun die Punkte N und M miteinander.
Du erhälst die Strecke NM.
Markiere die Hälfte der Strecke NM.
Es entsteht der Punkt P.
Verbinde nun die Punkte A und P miteinander.
Du erhälst die Strecke AP.
Diese Strecke AP ist die Winkelhalbierende des Winkels BAC.
Bemerkungen zur "Lösung" von Celebino
Die Lösung ist falsch.--*m.g.* 10:26, 13. Jul. 2011 (CEST)
Sie würde nur funktionieren, wenn  ein gleichschenkliges Dreieck mit
ein gleichschenkliges Dreieck mit 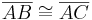 wäre.
wäre.

