Zu den Lösungsversuchen
Inhaltsverzeichnis |
Aufgabe 3.1
(alles in ein und derselben Ebene)
Es sei  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  und dem Radius
und dem Radius  . Ferner sei
. Ferner sei  eine Gerade, die durch den Mittelpunkt von k geht. Schließlich sei
eine Gerade, die durch den Mittelpunkt von k geht. Schließlich sei  der gemeinsame Schnittpunkt der Senkrechten in
der gemeinsame Schnittpunkt der Senkrechten in  auf
auf  mit
mit  . Wir definieren eine Abbildung
. Wir definieren eine Abbildung  von
von 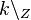 auf
auf  :
: 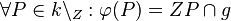 . Ist
. Ist  fixpunktfrei?
fixpunktfrei?
Es scheint sich daraufhin herauszulaufen, dass die Schnittpunkte A und B aus 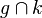 Fixpunkte bzgl.
Fixpunkte bzgl.  sind. --Flo60 16:58, 13. Nov. 2011 (CET)
sind. --Flo60 16:58, 13. Nov. 2011 (CET)
Aufgabe 3.2
Es sei 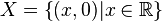 . Wir definieren auf
. Wir definieren auf 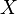 die folgende Abbildung
die folgende Abbildung  :
: 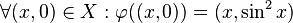 . Jedes Element des
. Jedes Element des 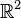 fassen wir als Punkt auf. Hat
fassen wir als Punkt auf. Hat  Fixpunkte? Wenn ja welche? (Geogebra hilft)
Fixpunkte? Wenn ja welche? (Geogebra hilft)
Also auch hier sieht es so aus, als hätten  eine unendliche Anzahl von Fixpunkten oder anders ausgedrückt: sin(x) besitzt bzgl.
eine unendliche Anzahl von Fixpunkten oder anders ausgedrückt: sin(x) besitzt bzgl. 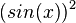 identische Werte für alle
identische Werte für alle 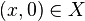 .
.
Allerdings habe ich mich persönlich in meinem Leben bisher wenig mit Sinusfunktionen auseinandergesetzt (kurz auf der Realschule um am Dreieck herumzurechnen). Und einfach nur Funktionen im Geogebra eingeben ist auch nicht so der Renner, wenn man nicht weiß, woher sie kommen. Vielleicht kann mal jemand eine Applikation einstellen, die den ganzen Spaß verdeutlicht - dann braucht man nicht lange in der Literatur herumzusuchen.
Aufgabe 3.3
Unter der Menge aller Punkte wollen wir die Menge aller Pixel eines LCD-Bildschirms  mit FullHD-Auflösung (1920 x 1080) verstehen. Jedes dieser Pixel
mit FullHD-Auflösung (1920 x 1080) verstehen. Jedes dieser Pixel  hat bezüglich eines bildschirmeigenen Koordinatensystems die Koordinaten
hat bezüglich eines bildschirmeigenen Koordinatensystems die Koordinaten 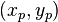 . Wir definieren auf den Pixeln unseres Bildschirms
. Wir definieren auf den Pixeln unseres Bildschirms  die folgende Abbildung
die folgende Abbildung  :
: 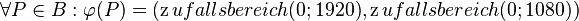 . Wie groß ist die Wahrscheinlichkeit, dass
. Wie groß ist die Wahrscheinlichkeit, dass  einen Fixpunkt hat?
einen Fixpunkt hat?
| 1 | 2 | |
| Nr. | Beschreibung des Schrittes | Begründung der Korrektheit des Schrittes |
|---|---|---|
| 1. | 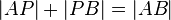
|
gilt, wegen der Relation zwischen. |
| 2. | 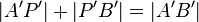
|
Relation zwischen bleibt nach der Ausführung der Bewegung erhalten. |
| 3. | 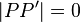 --> P=P' --> P=P'
|
folgt aus (1.) und (2.) und der Vss, dass A und B Fixpunkte sind. |
Deshalb wird auch Punkt P bei der Bewegung auf sich selbst abgebildet.
(Ich bin mir nicht sicher, ob ich alles bedacht habe, vielleicht kann noch jemand was dazu sagen/korrigieren. Warum bei der Tabelle über der Spaltenbeschriftung noch 1. und 2. steht ist mir auch schleierhaft.) Pipi Langsocke 12:05, 10. Nov. 2011 (CET)
Aufgabe 3.5
Beweisen Sie: Wenn drei nicht kollineare Punkte  Fixpunkte der Bewegung
Fixpunkte der Bewegung  sind, so ist
sind, so ist  die identische Abbildung.
die identische Abbildung.
 und
und  eine Fixpunktgerade bezüglich
eine Fixpunktgerade bezüglich