12)
Inhaltsverzeichnis |
Aufgabe 15.1
Frau Schultze räumt ihren Schrank auf. Es findet sich ein Stapel Arbeitsblätter, auf die ein Parallelogramm gedruckt wurde, welches keine Raute ist. "Zu dumm", denkt Frau Schultze, "ich brauche Arbeitsblätter mit Rauten". Kurz darauf kommt ihr eine zündende Idee. Sie wird den Begriff der Raute konstruktiv erarbeiten lassen. Diesbezüglich wird sie den Schülern den Auftrag geben, die Parallelogramme auf den vorhandenen Arbeitsblättern auszuschneiden und dann so zu falten, dass zwei benachbarte Seiten des Parallelogramms zur Deckung kommen. Erläutern Sie wie und beweisen Sie dass die Schüler von Frau Schultze durch die genannten Faltungen aus den Parallelogrammen Rauten generieren.
Lösung von Aufg. 15.1 (WS_11/12)
Aufgabe 15.2
Es seien  ein Quadrat und
ein Quadrat und  eine positive reelle Zahl, die kleiner als die Seitenlänge von
eine positive reelle Zahl, die kleiner als die Seitenlänge von  ist. Ferner seien die Punkte
ist. Ferner seien die Punkte 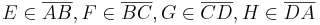 mit
mit 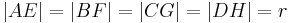 gegeben. Man beweise:
gegeben. Man beweise: 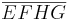 ist ein Quadrat.
ist ein Quadrat.
Lösung von Aufg. 15.2 (WS_11/12)
Aufgabe 15.3
Nennen Sie eine Umkehrung des Satzes von Thales und beweisen Sie diese.
Lösung von Aufg. 15.3 (WS_11/12)
Aufgabe 15.4
Wir gehen von folgender Definition aus: Ein Drachen ist ein Viereck mit zwei Paaren jeweils zueinander kongruenter benachbarter Seiten. Beweisen Sie den folgenden Satz: Wenn 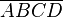 ein konvexer Drachen mit
ein konvexer Drachen mit 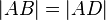 ist, dann sind die Strahlen
ist, dann sind die Strahlen 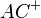 und
und 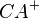 die Winkelhalbierenden von
die Winkelhalbierenden von 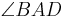 und
und 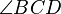 .
.

