Übung Aufgaben 3 (SoSe 12)
Inhaltsverzeichnis |
Aufgaben zur Inzidenz in der Ebene
Aufgabe 3.1
Es sei P die Menge der Punkte und G die Menge der Gerade. Wir betrachten folgendes Modell:
P = {A,B,C,D}
G = {{A,B}, {A,C}, {A,D}, {B,C}, {B,D}, {C,D}}
a) Veranschaulichen Sie das Modell durch eine Skizze.
b) Sind bei dem Modell die Axiome I.0 bis I.3 erfüllt?
Lösung von Aufgabe 3.1 (SoSe_12)
Aufgabe 3.2
Hier finden Sie Aufgabe 3.2.
Lösung von Aufgabe 3.2 (SoSe_12)
Aufgabe 3.3
Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.
- Wir formulieren Satz I neu und beginnen mit „Es seien
 ,
,  und
und  drei Punkte.“ Ergänzen Sie: „Wenn
drei Punkte.“ Ergänzen Sie: „Wenn  ,
, und
und  … , dann … .“
… , dann … .“
- Beweisen Sie Satz I indirekt.
- Bilden Sie die Kontraposition von Satz I.
- Beweisen Sie auch die Kontraposition von Satz I.
- Formulieren Sie die Umkehrung von Satz I.
- Gilt auch die Umkehrung von Satz I?
Lösung von Aufg. 3.3 (SoSe_12)
Aufgaben zur Inzidenz im Raum
Die Inzidenzaxiome können für die Geometrie im Raum erweitert werden. Lesen Sie sich hier die Inzidenz im Raum SoSe_12) durch, Sie benötigen die Axiome und Definitionen für die folgenden Aufgaben.
Aufgabe 3.R
Das Axiom I.7 sagt aus:
Es gibt vier Punkte, die nicht komplanar sind.
Es sei  eine beliebige Ebene und
eine beliebige Ebene und  die vier Punkte entsprechend Axiom I.7. Klassifizieren Sie alle Fälle die bezüglich der Inzidenz der Punkte
die vier Punkte entsprechend Axiom I.7. Klassifizieren Sie alle Fälle die bezüglich der Inzidenz der Punkte  mit
mit  auftreten können.
auftreten können.
Lösung von Aufg. 3.R (SoSe_12)
Aufgabe 3.Q
Beweisen Sie Satz I.6: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
Lösung von Aufg. 3.Q (SoSe_12)
Aufgabe 3.Y
Satz:
- Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.
- Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
- Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
- Beweisen Sie den Satz. Hier ein Anfang für den Beweis:
Beweis
- Es seien
 und
und 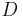 vier Punkte, die nicht komplanar sind.
vier Punkte, die nicht komplanar sind.
- Es seien
zu zeigen
- ...
Annahme:
- Es gibt drei Punkte von den vier Punkten
 , die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
- Es gibt drei Punkte von den vier Punkten
Lösung von Aufg. 3.Y (SoSe_12)
Aufgabe 3.W
Es sei  eine Gerade und
eine Gerade und  ein Punkt, der nicht zu
ein Punkt, der nicht zu  gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene
gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene  , die sowohl alle Punkte von
, die sowohl alle Punkte von  als auch den Punkt
als auch den Punkt  enthält.
enthält.
Lösung von Aufg. 3.W (SoSe_12)
Aufgabe 3.E
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung den Satz aus Aufgabe 6.6).
Lösung von Aufg. 3.E (SoSe_12)
Aufgabe 3.T
Beweisen Sie Satz I.5 : Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen.
Lösung von Aufg. 3.T (SoSe_12)
Aufgabe 3.Z
Beweisen Sie Satz I.7 : Jede Ebene enthält (wenigstens) drei Punkte.

