Übung Aufgaben 5 (SoSe 12)
Inhaltsverzeichnis |
Aufgaben zum Abstand
Aufgabe 4.1
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Lösung von Aufgabe 4.1 (SoSe_12)
Aufgabe 4.2
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:





Tipps zu Aufgabe 4.2 (SoSe_12)
Lösung von Aufgabe 4.2 (SoSe_12)
Aufgabe 4.3
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:
Wenn 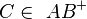 und
und 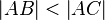 dann gilt
dann gilt 
Lösung von Aufgabe 4.3 (SoSe_12)
Aufgabe 4.4
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  auf
auf  mit
mit 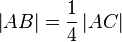 und
und 


Tipps zu Aufgabe 4.4 (SoSe_12)
Lösung von Aufgabe 4.4 (SoSe_12)
Weitere Aufgaben zur Inzidenz
Aufgabe 4.5
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 3.3 und 3.5).
Aufgabe 4.6
Es sei  eine Gerade und
eine Gerade und  ein Punkt, der nicht zu
ein Punkt, der nicht zu  gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene
gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene  , die sowohl alle Punkte von
, die sowohl alle Punkte von  als auch den Punkt
als auch den Punkt  enthält.
enthält.
Lösung von Aufgabe 4.6_S (SoSe_12) Lösung von Aufg. 4.5 (SoSe_12)

