Lösung von Aufgabe 5.2 S (SoSe 12)
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:





Tipps zu Aufgabe 5.2 (SoSe_12)
Inhaltsverzeichnis |
Lösung von RitterSport
Version a
| Schritt | Aktion |
|---|---|
| (1) | Zw (A,B,C) |
| (2) | VxE .xE .xE UND (VxE UND (VxE .xE .xE ODER xnichtE ODER xnichtE ) )
|
| (3) |  c c 
|
Wie schreibt man bloß diese Formeln? (außer zu kopieren)^^
--RitterSport 16:44, 20. Mai 2012 (CEST)
Version b
Wäre Folgendes möglich?
Wegen Axiom I/1: 
Wegen Zw (A,B,C): | | + |
| + | | = |
| = | |
|
Somit ist  c
c 
Da ist was wahres dran, überzeugt mich so jedoch noch nicht.--*m.g.* 17:56, 20. Mai 2012 (CEST)
--RitterSport 16:56, 20. Mai 2012 (CEST)
Hinweise von M.G. zu LaTex
Schön, dass Sie sich an die LaTex-Syntax herantrauen. Kleine Motivationshilfe: Sie können diese Syntax auch in den modernen Wordversionen und natürlich in Open Office verwenden. LaTex selbst ist ein Textsystem für mathematische Texte, das Freeware ist. In LaTex selbst wird der Beginn und das Ende einer mathematischen Formel durch das Dollarzeichen gekennzeichnet. Hier in der Wikiseitenbeschreibungssprache verwenden wir nicht das Dollarzeichen sondern die Tags<math> </math>.
Eine umfassende Hilfe zu LaTex im Rahmen des Wikis finden sie hier [1]
Wenn Sie irgend etwas Bestimmtes suchen können Sie auch googeln: Nehmen wir an, Sie suchen das Zeichen für "für alle x": Geben Sie in Google die Suche "für alle x LaTex" ein und Sie sollten recht schnell fündig werden.
Hinweise von M.G. zu den Lösungsversuchen von RitterSport
Irgendwie scheinen Sie selbst noch nicht ganz überzeugt von Ihren Beweisen. Sie müssen die im übrigen nicht so formal schreiben, sie dürfen auch textliche Sätze (o-Ton von meinem ehemaligen Chemielehrer) verwenden.
Also ich versuche es mal:
Es seien 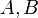 und
und  drei paarweise verschiedene Punkte, von denen der Punkt
drei paarweise verschiedene Punkte, von denen der Punkt  zwischen den beiden anderen Punkten, also
zwischen den beiden anderen Punkten, also  und
und  , liegt.
, liegt.
Zeigen sollen wir, dass nun die Strecke  eine Teilmenge der Strecke
eine Teilmenge der Strecke  ist.
ist.
Dieses hätten wir gezeigt, wenn wir nachgewiesen hätten, dass jeder Punkt von .... auch ein Punkt ..... (ergänzen Sie selbst.)
Es sei nun  ein beliebiger Punkt der Strecke
ein beliebiger Punkt der Strecke  .
.
Weil  zur Strecke
zur Strecke  gehört, liegt er entsprechend der Definition des Begriffs Strecke zwischen den beiden Punkten .... (ergänzen Sie wieder selbst)
gehört, liegt er entsprechend der Definition des Begriffs Strecke zwischen den beiden Punkten .... (ergänzen Sie wieder selbst)
Da nun der Punkt  zwischen den Punkten .... liegt, gilt entsprechend der Definition der Zwischenrelation die folgende Gleichung:
zwischen den Punkten .... liegt, gilt entsprechend der Definition der Zwischenrelation die folgende Gleichung:
....
Zeigen wollen wir, das  auch zwischen .... liegt.
auch zwischen .... liegt.
Entsprechend der Definition der Zwischenrelation wäre letzteres der Fall, wenn die Gleichung ... gelten würde.
Für den Nachweis der Gültigkeit der obigen Gleichung dürfen wir die Voraussetzung, dass  zwischen
zwischen  und
und  liegt verwenden. Als Gleichung ausgedrückt stellt sich diese Voraussetzung wie folgt dar: ....
liegt verwenden. Als Gleichung ausgedrückt stellt sich diese Voraussetzung wie folgt dar: ....
Jetzt haben Sie zwei Gleichungen, von denen Sie ausgehen dürfen und eine deren Gültigkeit Sie nachweisen müssen. Wenn Sie wissen, welche Gleichungen das sind, sollte der Beweis kein Problem mehr sein. Viel Erfolg! --*m.g.* 17:55, 20. Mai 2012 (CEST)


