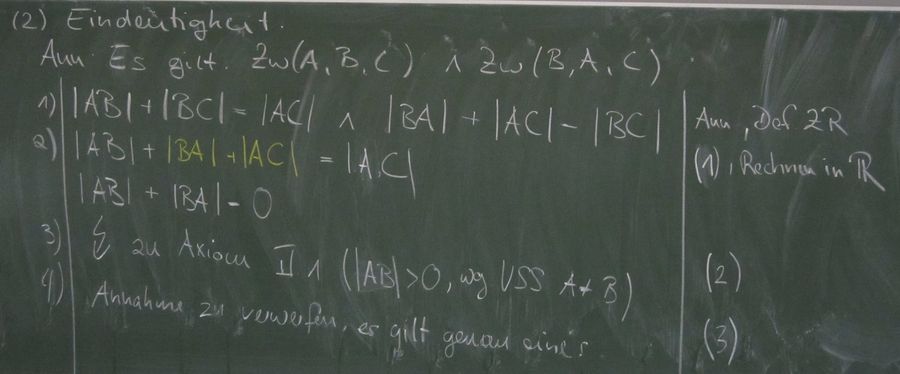Lösungsideen Übung Heckl 23.05.2012

Aufgabe 5.1

Satz:

Von drei paarweise verschiedenen Punkten $\ A, B$ und $\ C$ ein und derselben Geraden $\ g$ liegt genau einer zwischen den beiden anderen.

Die Behauptung wurde auf zwei verschiedene Arten und Weisen formuliert!

Diese gelben 'Häckchen' sind in Wirklichkeit keine 'Häckchen', sondern bedeuten das aussagelogische ODER ($\vee$)

--Flo60 21:29, 23. Mai 2012 (CEST)

Aufgabe 5.3

Zeigen Sie, dass für drei paarweise verschiedene Punkte $\ A, B$ und $\ C$ gilt:
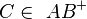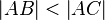Wenn $C \in \ AB^{+}$ und $\left| AB \right| < \left| AC \right|$ dann gilt $\operatorname Zw (A, B, C)$

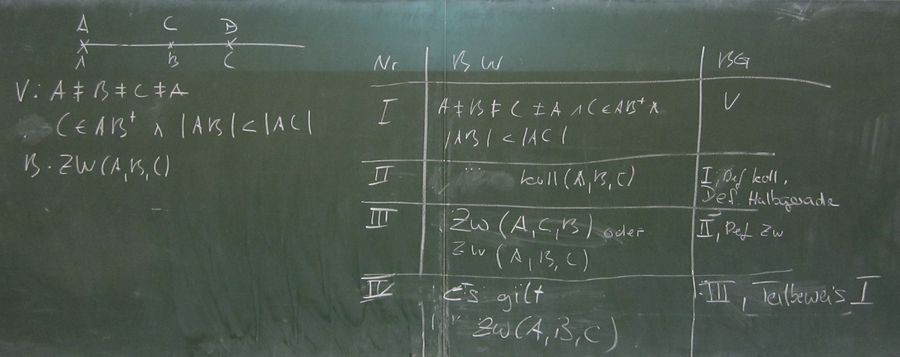
Schritt III müsste eigentlich noch ergänzt werden mit der Begründung, warum nur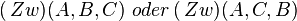 $\operatorname(Zw) (A, B, C) \ oder \operatorname(Zw) (A, C, B)$ 

gelten kann (Definition Halbgerade; A ist Anfangspunkt).

--Flo60 21:33, 23. Mai 2012 (CEST)

Platz für Kommentare zu Aufgabe 5.2

Ich bin den Beweis noch einmal durchgegangen. Dabei sind mir 2 Dinge aufgefallen:
1. Müssten wir der Vollständigkeit halber bei Schritt 2 nicht auch koll(A,B,C) sagen?
2. Fehlt uns nicht ein Schritt zwischen (2) und (3), nämlich /AB/ + /BC/ = /AC/, /AC/ + /CB/ = /AB/ mit der Begründung Ax. II.2 und (2)? Denn nur daraus können wir jetzt mit der Def. Zw den Schritt (3) herleiten (Oder?)

Aufgabe 5.5

Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).

Ein bereitgestelltes Skript einer Übungsteilnehmerin - dankeschön

Aus der Übung

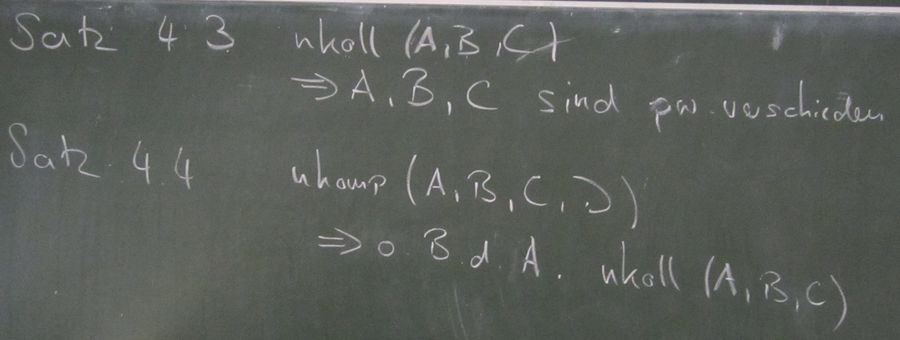
--Flo60 21:45, 23. Mai 2012 (CEST)

Zurück zur Übungsseite

Übung Aufgaben 5 S (SoSe 12)