Lösung von Aufgabe 9.3 S

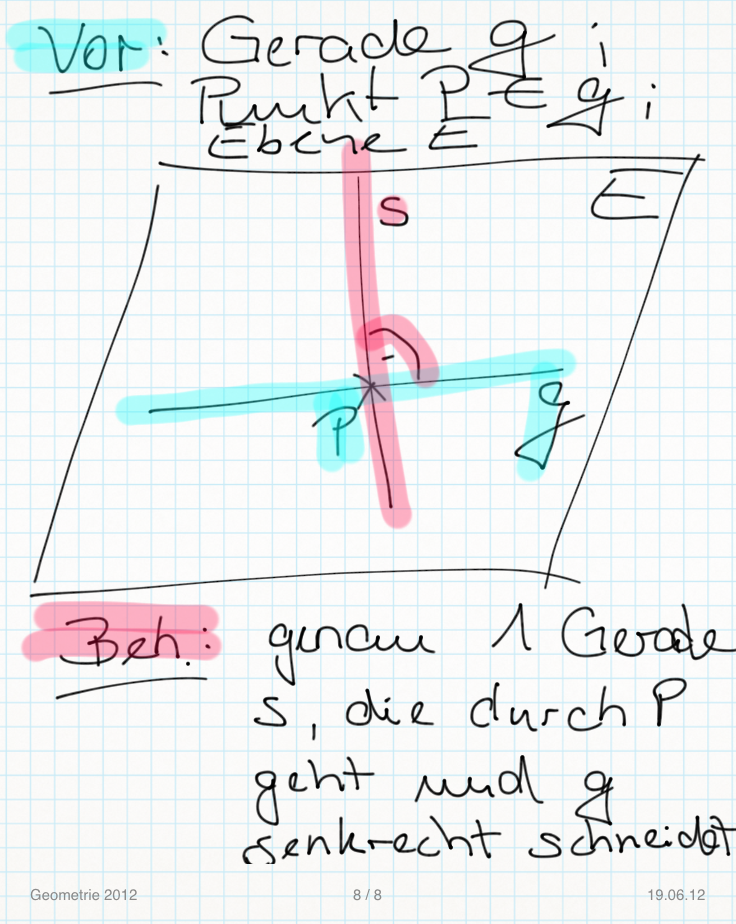
Satz:
Es sei $g$ eine Gerade der Ebene $E$. Ferner sei $P$ ein Punkt auf $g$. In der Ebene $E$ gibt es genau eine Gerade $s$, die durch $P$ geht und senkrecht auf $g$ steht.

Beweisen Sie den Satz.

Lösungsversuch Nummero6/Tchu Tcha Tcha:

Eindeutigkeitsbeweis..Beweisen durch Widerspruch!
Annahme: Es gibt 2 nicht identische Geraden, die durch den Punkt P gehen und g senkrecht schneiden.
Fortsetzung folgt...--Tchu Tcha Tcha 16:56, 20. Jun. 2012 (CEST)