Lösung von Aufgabe 9.5 S

Satz:
Es sei 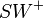$\ SW^{+}$ die Winkelhalbierende des Winkels $\angle ASB$. Dann gilt:
$\left| \angle ASW \right| = \left| \angle WSB \right| = \frac{1}{2} \left|\angle ASB\right|$

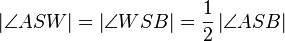
Beweisen Sie den Satz.

Skizze:

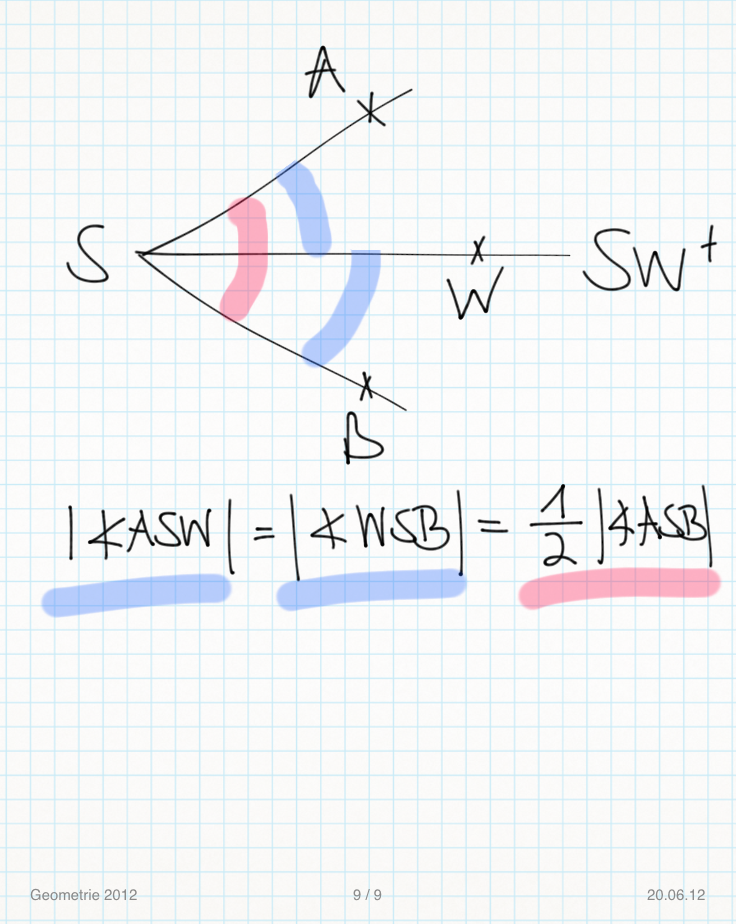
Voraussetzung 1: $\angle ASB$
Voraussetzung 2: 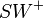$\ SW^{+}$ ist die Winkelhalbierende des Winkels $\angle ASB$
Behauptung: 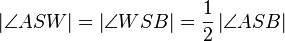$\left| \angle ASW \right| = \left| \angle WSB \right| = \frac{1}{2} \left|\angle ASB\right|$

(1) Da nach Vor. 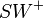$\ SW^{+}$ die Winkelhalbierende des Winkels $\angle ASB$ ist, gilt: $\left| \angle ASW \right| = \left| \angle WSB \right|$
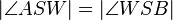
(2) Nach Vor. und Def. Winkelhalbierende muss W im Inneren des Winkels $\angle ASB$ liegen.
(3) Nun wissen wir nach dem Winkeladditionsaxiom und (1), dass gelten muss: 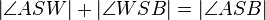$\left| \angle ASW \right| + \left| \angle WSB \right| = \left| \angle ASB \right|$.
(4) Nach (1) können wir (3) auch folgendermaßen schreiben: 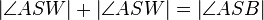$\left| \angle ASW \right| + \left| \angle ASW \right| = \left| \angle ASB \right|$.
(5) Nach (4) und Rechnen in R folgt: 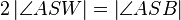$2 \left| \angle ASW \right| = \left| \angle ASB \right|$.
(6) Nach (5),(1) und Rechnen in R folgt: 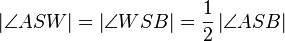$\left| \angle ASW \right| = \left| \angle WSB \right| = \frac{1}{2} \left|\angle ASB\right|$
Behauptung stimmt.
qed --Tchu Tcha Tcha 18:57, 20. Jun. 2012 (CEST)

Lösung Kopernikus; Just noch ein sailA

Vor:

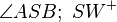$\angle ASB ; \ SW^{+}$ ist Winkelhalbierende ;

Beh:

$\angle \left| ASW\right| =\angle \left| WSB \right| =\angle \frac{1}{2} \left| ASB \right|$

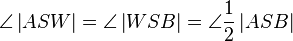
Schritt	Beweis	Begründung
1	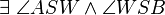$\exists \ \angle ASW \wedge \angle WSB$	Vor; Def. VI1.2 (Def. Winkelhalbierende)
2	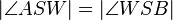$\left| \angle ASW \right| =\left| \angle WSB \right|$	Def. VI1.2 (Def. Winkelhalbierende)
3	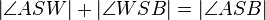$\left| \angle ASW \right| +\left| \angle WSB \right| =\left| \angle ASB \right|$	Axiom IV.3 (Winkeladditionsaxiom)
4	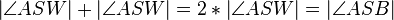$\left| \angle ASW \right| +\left| \angle ASW \right| =2*\left| \angle ASW \right|= \left| \angle ASB \right|$	Rechnen in R
5	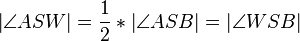$\left| \angle ASW \right| =\frac{1}{2} *\left| \angle ASB \right|= \left| \angle WSB \right|$	Rechnen in R
6	q.e.d	Vor; 5

--Kopernikus 19:37, 26. Jun. 2012 (CEST)
--Just noch ein sailA 19:37, 26. Jun. 2012 (CEST)

Kann ich annehmen, dass die Winkelhalbierende im Inneren des Winkels <ASB liegt, oder müsste man beweisen, dass SW+ tatsächlich im Inneren liegt?? Die Definition Winkelhalbierende sagt ja nur aus, "wenn die Halbgerade im Inneren liegt". Ebenso heißt es im Winkeladditionsaxiom "wenn P im Inneren des Winkels liegt". Das Wörtchen "wenn" irritiert mich gerade ein bisschen! Hoffe mir kann jemand helfen. --Mahe84 13:23, 27. Jun. 2012 (CEST)