|
Satz XI. 1: (Existenz von Parallelen)
- Zu jedem Punkt
 außerhalb einer Geraden außerhalb einer Geraden  gibt es eine Gerade gibt es eine Gerade  , die durch , die durch  geht und parallel zu geht und parallel zu  ist. ist.
Beweis der Existenz von Parallelen
Übungsaufgabe
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Skizze folgt..
(1) Nach der Ex. & Eind. des Lots gibt es eine Gerade durch P, welche senkrecht zu g ist.
(2) 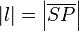 // Vor., (1), Abstandsaxiom // Vor., (1), Abstandsaxiom
(3) Es gibt einen weiteren Punkt 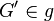 mit mit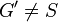 // Vor., Axiom I.2 // Vor., Axiom I.2
(4) Es gibt genau einen Strahl 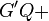 in der HE G'S,P+ mit in der HE G'S,P+ mit 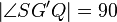 // Winkelkonstruktionsaxiom // Winkelkonstruktionsaxiom
(5) es gibt genau einen Punkt P_2 auf 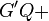 mit mit 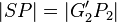 // Axiom v. Lineal, (4),(2) // Axiom v. Lineal, (4),(2)
(6) 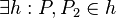 // Vor., (5), Axiom I.1 // Vor., (5), Axiom I.1
(7) qed?!? (oder muss noch bewiesen werden, dass alle Punkte der Geraden h denselben Abstand zur Geraden g haben?!? eigentlich trivial, oder? :-) )
--Tchu Tcha Tcha 15:20, 10. Jul. 2012 (CEST)
Die Eindeutigkeit ("Zu jedem Punkt  außerhalb einer Geraden außerhalb einer Geraden  gibt es höchstens eine Gerade gibt es höchstens eine Gerade  , die durch , die durch  geht und parallel zu geht und parallel zu  ist.") kann in der absoluten Geometrie nicht bewiesen werden. Wir müssen die Eindeutigkeit der Parallelen axiomatisch fordern. Das entsprechende Axiom heißt Euklidisches Parallelenaxiom (EP). Sobald das EP gilt, befinden wir uns nichtmehr in der absoluten Geometrie, sondern in der euklidischen. ist.") kann in der absoluten Geometrie nicht bewiesen werden. Wir müssen die Eindeutigkeit der Parallelen axiomatisch fordern. Das entsprechende Axiom heißt Euklidisches Parallelenaxiom (EP). Sobald das EP gilt, befinden wir uns nichtmehr in der absoluten Geometrie, sondern in der euklidischen.
|