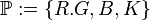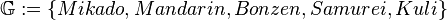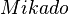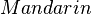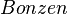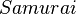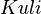|
Aufgabe 5.2
Gegeben seien eine rote Kugel aus Knete ( ), eine blaue Kugel aus Knete ( ), eine blaue Kugel aus Knete ( ), eine grüne Kugel aus Knete ( ), eine grüne Kugel aus Knete ( ) und eine schwarze Kugel aus Knete ( ) und eine schwarze Kugel aus Knete ( ). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai. ). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.
Wir betrachten das folgende Modell für die Inzidenz:
- Menge aller Punkte
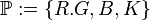
- Menge aller Geraden
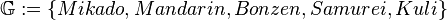
Die Inzidenzrelation interpretieren wir wie folgt: Ein Modellpunkt inziert mit einer Modellgeraden, wenn der Modellpunkt auf die Modellgerade gesteckt wurde.
Wir lassen die Modellpunkte mit den Modellgeraden jetzt wie folgt inzidieren:
-
 und und  inzidieren mit inzidieren mit 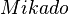
-
 und und  inzidieren mit inzidieren mit 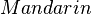
-
 und und  inzidieren mit inzidieren mit 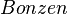
-
 und und  inzidieren mit inzidieren mit 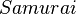
-
 und und  inzidieren mit inzidieren mit 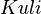
| (a) |
Fertigen Sie eine Skizze für dieses Modell an bzw. stellen Sie ein Foto von einem real gebauten Modell hier ein.
|
| (b) |
Nennen Sie drei verschiedene Gründe, warum dieses Modell kein Modell für die Inzidenzaxiome des Raumes ist.
|
| (c) |
Ergänzen Sie das Modell Sie derart, dass die Inzidenzaxiome I.1 bis I.7 erfüllt sind.
|
| (d) |
Mit dem von Ihnen ergänzten Modell haben Sie gezeigt, dass das Axiom I.0 unabhängig von den Axiomen I.1 bis I.7 ist. Warum?
|
| (e) |
Beweisen Sie: Wählt man zu unseren Knetekugeln als Modellgeraden Stäbchen eines originalen Mikadospiels derart, dass sich alle Geraden paarweise unterscheiden, so kann man kein Modell für die Inzidenzaxiome des Raumes bauen.
|
Lösung von User...
Lösung von User ...
|
 ), eine blaue Kugel aus Knete (
), eine blaue Kugel aus Knete ( ), eine grüne Kugel aus Knete (
), eine grüne Kugel aus Knete ( ) und eine schwarze Kugel aus Knete (
) und eine schwarze Kugel aus Knete ( ). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.
). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.