Lösung von Aufgabe 6.1 S (WS 12 13)
Aus Geometrie-Wiki
Version vom 3. Dezember 2012, 13:23 Uhr von *m.g.* (Diskussion | Beiträge)
Aufgabe 6.1
Satz:
- Es seien
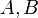 und
und  drei paarweise verschiedene Punkte.
drei paarweise verschiedene Punkte.
- Wenn der Punkt
 zwischen den Punkten
zwischen den Punkten  und
und  liegt, dann liegt weder
liegt, dann liegt weder  zwischen
zwischen  und
und  noch
noch  zwischen
zwischen  und
und  .
.
- Es seien
Beweisen Sie diesen Satz.
Lösung 6.1 von User Hazel12
Ich denke, dass die Voraussetzung ist, dass die 3 Punkte paarweise verschieden sind, also:
Vor: A,B,C sind paarweise verschieden Beh: Zw(A,B,C) Ann: Zw(A,B,C) und (oBdA.) Zw(B,A,C)
Wenn man doch oBdA. hinschreibt, muss man den zweiten Teil des Beweises nicht mehr machen, oder?--Sissy66 14:23, 2. Dez. 2012 (CET)


