Serie 05 12 13
Aus Geometrie-Wiki
Version vom 15. Dezember 2012, 18:48 Uhr von *m.g.* (Diskussion | Beiträge)
Aufgabe 5.1
Es sei 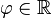 .
.
Wir definieren die folgende Abbildung 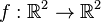
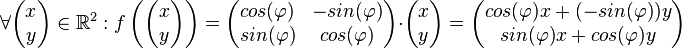 .
.
Beweisen Sie:  ist eine lineare Abbildung.
ist eine lineare Abbildung.
Interpretieren Sie  geometrisch.
geometrisch.
Hilfe:
Aufgabe 5.2
Es sei 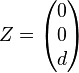 ,
,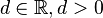
Es sei  die
die 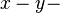 Ebene, die wir wiederum als
Ebene, die wir wiederum als 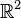 interpretieren. Wir bilden jedes Element des
interpretieren. Wir bilden jedes Element des 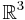 mittels der Abbildung
mittels der Abbildung 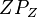 auf
auf  wie folgt ab:
wie folgt ab:
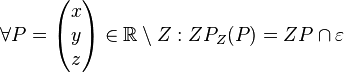 .
.
Beweisen Sie: 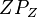 ist linear.
ist linear.
Aufgabe 5.3
Geben sei  eine Menge, die aus folgenden Vektoren des
eine Menge, die aus folgenden Vektoren des 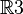 besteht:
besteht:
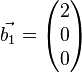 ,
, 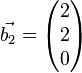 ,
, 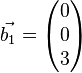
Beweisen Sie: Jedes 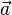 aus
aus 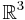 lässt sich als Linearkombination der Vektoren der Menge
lässt sich als Linearkombination der Vektoren der Menge  darstellen.
darstellen.

