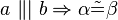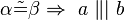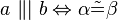Lösung von Aufgabe 3.3 (SoSe 13 P)

a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel $\alpha$ und $\beta$. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?

1. $\ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta$

• Es fehlt der Bezug zur Gerade c.--Nolessonlearned 17:13, 7. Mai 2013 (CEST)
  
  • Diese Aussage repräsentiert den Stufenwinkelsatz.--Nolessonlearned 14:29, 10. Mai 2013 (CEST)
    
    • So ist es.--Tutorin Anne 21:42, 11. Mai 2013 (CEST)

1. $\alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b$

• Umkehrung von (1). Gleiche Problematik wie in (1).--Nolessonlearned 17:13, 7. Mai 2013 (CEST)
  
  • Hierbei handelt es sich um die Umkehrung der oberen Implikation. Eine Umkehrung des Stufenwinkelsatzes ist jedoch nicht möglich, daher ist diese Implikation weder repräsentativ noch äquivalent zum Stufenwinkelsatz.--Nolessonlearned 14:29, 10. Mai 2013 (CEST)
    
    • Gut begründet und nur noch ein Fehler.--Tutorin Anne 21:42, 11. Mai 2013 (CEST)
      • Komme nicht drauf.--Nolessonlearned 16:24, 12. Mai 2013 (CEST)
        
        • Die Aussage ist sehr wohl wahr. Sie muss aber extra bewiesen werden, da sie eben nicht äquivalent zum Stufenwinkelsatz ist.--Tutorin Anne 10:28, 23. Mai 2013 (CEST)

1. $\|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b$

• Äquivalente Aussage zum Stufenwinkelsatz. Logischer Zusammenhang.--Nolessonlearned 16:59, 7. Mai 2013 (CEST)
  
  • Hierbei handelt es sich um eine Kontraposition zu dem Stufenwinkelsatz. --Nolessonlearned 14:29, 10. Mai 2013 (CEST)
    
  • Äquivalente Aussage zum Stufenwinkelsatz.--Nolessonlearned 18:18, 10. Mai 2013 (CEST)
    

 ** könnte jemand dies mal ohne Formelzeichen in einen Satz schreiben, ich versteh die ganzen Zeichen gar nicht und deswegen auch nicht die Aussage --Grashalm 11:36, 12. Jun. 2013 (CEST)

Hallo Grashalm, hier einmal in Worten:

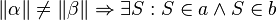1. $\|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b$ bedeutet: Wenn das Maß des Winkels alpha ungleich dem Maß des Winkels beta, dann existiert ein Punkt S für den gilt: S ist element von a und S ist element von b.
   

Hilft dir das weiter?
--TobiWan 16:22, 12. Jun. 2013 (CEST)

ja vielen dank, nun kann ich es nachvollziehen :) --Grashalm 18:25, 12. Jun. 2013 (CEST)

1. $\ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta$

• Selbe Problematik wie in (1) und (2).--Nolessonlearned 17:13, 7. Mai 2013 (CEST)
  
  • Da eine Umkehrung des Stufenwinkelsatzes nicht möglich ist (siehe 2. Implikation), ist eine Äquivalenzrelation der beiden Aussagen ebenfalls ausgeschlossen.--Nolessonlearned 18:18, 10. Mai 2013 (CEST)
    
    • Mh, stimmt nicht ganz.--Tutorin Anne 21:42, 11. Mai 2013 (CEST
      )
      • Bräuchte etwas Hilfe. Komme nicht drauf. --Nolessonlearned 16:24, 12. Mai 2013 (CEST)
        
        • Siehe 2)--Tutorin Anne 10:28, 23. Mai 2013 (CEST)
          • Wenn man also die 2.Implikation beweist, dann gilt auch diese Äquivalenzrelation oder? --Zweieck 14:03, 30. Mai 2013 (CEST)
            • So ist es.--Tutorin Anne 18:24, 2. Jun. 2013 (CEST)

Also zusammenfassend habe ich das jetzt so verstanden|:

1.) Stufenwinkelsatz 2.) Umkehrung des Stufenwinkelsatzes; aber nicht gültig, da noch nicht bewiesen 3.) Kontraposition des Stufenwinkelsatzes; gilt da Kontraposition immer Äquivalent zum ursprünglichen Satz 4.) Äquivalenz des Stufenwinkelsatzes; gilt erst wenn die Umkehrung bewiesen wurde --Wüstenfuchs 12:44, 4. Jul. 2013 (CEST)