Benutzer:Tutorin Anne
Newsticker
Und Beobachtungsliste nicht vergessen!!
Extension:DynamicPageList (DPL), version 2.02 : Fehler: bei 'namespace' Parameter: 'Issue'! Hilfe: namespace= (leer) (Hauptnamensraum) | Benutzer | Benutzer_Diskussion | Campaign | Campaign_talk | Datei | Datei_Diskussion | Diskussion | Geometrie-Wiki | Geometrie-Wiki_Diskussion | Group | Group_talk | Hilfe | Hilfe_Diskussion | Kategorie | Kategorie_Diskussion | Layer | Layer_Diskussion | MediaWiki | MediaWiki_Diskussion | TimedText | TimedText_talk | Vorlage | Vorlage_Diskussion | Widget | Widget_Diskussion.
Mandala ganz einfach selbst gemacht!
Wo sich überall Mathematik verbirgt?!
Die Idee kam so
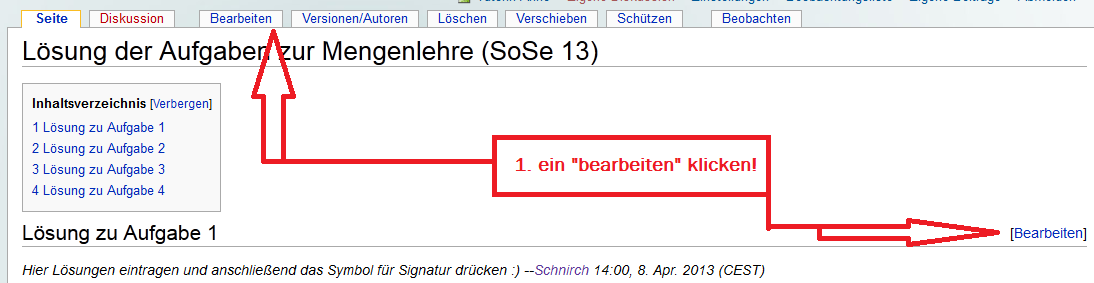
Anleitung: Mein erster Beitrag im Wiki
Nach dem ihr euch mit einem Fantasienamen angemeldet habt, könnt ihr Beiträge einfügen. Dabei kann man zunächst etwas Reinschreiben und das geht so:
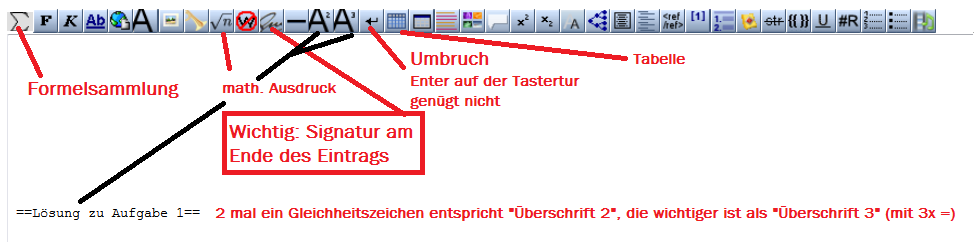
Die meisten Symbole sind ja selbsterklärend. Die Wichtigsten sind:
Nicht vergessen! Vor dem Speichern selbst das Layout mittels "Vorschau" überprüfen. Oft fehlen z.B. Zeilenumbrüche.
Am Rand findet ihr zur Orientierung die wichtigsten Dinge:
--Tutorin Anne 18:13, 16. Apr. 2013 (CEST)
Tabelle als Vorlage
| Voraussetzung | (V. hier eintragen) |
| Behauptung | (Beh. hier eintragen) |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | (Schritt 1 hier) | (Begründung 1) |
| 2 | (Schritt 2) | (Begründung 2) |
| 3 | (Schritt) | (Begründung) |
| 4 | (Schritt) | (Begründung) |
| Voraussetzung | ... |
| Behauptung | .... |
| Annahme | ... |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | ...) | ... |
| 2 | ... | ... |
| 3 | ... | ... |
| 4 | ... | ... |
| ... | ... | ... |
| ... | ... | ... |
Beweis: Parallelentreue der Geradenspiegelung Z9.1 SS2013
| Voraussetzung | a II b, 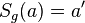 und und 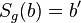
|
| Behauptung | a' II b' |
| Annahme | a' |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | 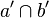 = {S'} = {S'} |
... |
| 2 | 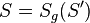 |
... |
| 3 | 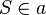 und und 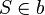 |
... |
| 4 | 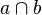 = {S} = {S} |
... |
| 5 | a' II b' | ... |
| 6 | Widerspruch zur Voraussetzung | ... |
WS12/13 Beweis zum Rechteck
Satz: Ein Rechteck hat 2 Symmetrieachsen.
| Voraussetzung | Rechteck 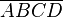
|
| Behauptung | 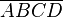 hat zwei Symmetrieachsen hat zwei Symmetrieachsen
|
Vorüberlegung: Es muss gezeicht werden, dass das Rechteck bei der Spiegelung an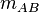 und
und 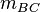 jeweils wieder auf sich abgebildet wird.
jeweils wieder auf sich abgebildet wird.
Beweisführung
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | m ist Mittelsenkrechte von  und n ist Mittelsenkrechte von und n ist Mittelsenkrechte von  |
Vor.; Def. Mittelsenkrechten |
| 2 | 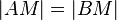 |
1.; Mittelsenkrechtenkriterium |
| 3 | 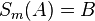 |
2.; Eigenschaften Geradenspiegelung (abstandserhaltend) |
| 4 | 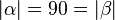 |
Vor. |
| 5 | 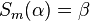 |
4. Eigenschaften Geradenspiegelung (Winkeltreue) |
| 6 | 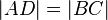 |
5. Vor. |
| 7 | 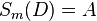 |
6. Eigenschaften Geradenspiegelung (abstandserhaltend) - müsste nicht Sm(D) = C sein? |
| 8 | 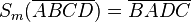 |
3.7. Eigenschaften Geradenspiegelung |
| 9 | m ist Symmetrieachse | 8. |
| 10 | n ist Symmetrieachse | analog Schritt 2-9 bezogen auf n |
Das ist jetzt mal so meine Idee, ich denke so könnte man es machen (mit richtiger Begründung!) - aber auch anders. Jetzt bitte Begründungen einfügen!!! --Tutorin Anne 18:58, 6. Feb. 2013 (CET)
SS12, Übung 10.3 Umkehrung des Basiswinkelsatzes, direkter Beweis
| Voraussetzung | Dreieck  mit üblicher Bezeichnung, mit üblicher Bezeichnung, 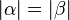
|
| Behauptung | 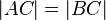
|
| Beweisschritt | Begründung |
|---|---|
1) m ist Mittelsenkrechte von  |
(Begründung 1) |
2) 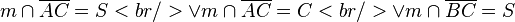 |
(Begründung 2) |
3) FAll 1)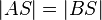 |
(Begründung) |
4) 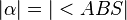 |
(Begründung) |
5) 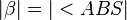 |
(Begründung) |
6) 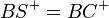 |
(Begründung) |
7) 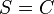 |
(Begründung) |
8) 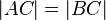 |
(Begründung) |
| 9) Fall 2) analog Fall 1 | - |
10) Fall 3) 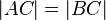 |
(Begründung) |
Funktionen (Elementare Funktionen SS 11)
Quadratische Funktion und ihr Graph, eine Parabel
Tutorium SS11
Tutorium 13, Aufgabe 1
| Voraussetzung | 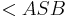 sei ein beliebiger Winkel sei ein beliebiger Winkel
|
| Behauptung | 1. Existenz einer Winkelhalbierenden 2. Eindeutigkeit dieser Wh |
Beweis zu 1.
z.z. Es exisitert ein Strahl 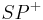 , für den gilt
, für den gilt 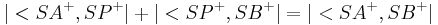 und
und 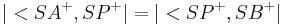 .
.
| 1) | 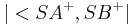 ist eine reele Zahl zwischen 0 und 180 ist eine reele Zahl zwischen 0 und 180 |
... |
| 2) | ... | ... |
| 3) | ... | ... |
| 4) | ... | ... |
| 5) | ... | ... |
Tutorium 3, Aufgabe 2