14)
Wie hoch muss ein Spiegel sein, damit Sie sich ganz darin sehen können und auf welcher Höhe muss die Oberkante des Spiegels angebracht werden? Anmerkung: Sie dürfen hier die Strahlensätze, wie sie aus der Schule bekannt sind, verwenden. Tipp: Hier finden Sie eine hilfreiche GeoGebra-Applikation.
- Gegeben sind die Bezeichnungen aus der verlinkten Geogebra-Applikation.
- Gegeben sind die Bezeichnungen aus der verlinkten Geogebra-Applikation.
- Aus den Strahlensätzen lässt sich herleiten:
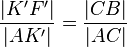 . (1)
. (1)
- Aus den Strahlensätzen lässt sich herleiten:
- Umformen ergibt:
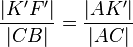 (2)
(2)
- Umformen ergibt:
- Aus den Eigenschaften der Geradenspiegelung ergibt sich:
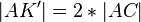 (3)
(3)
- Aus den Eigenschaften der Geradenspiegelung ergibt sich:
- Aus (2) und (3) folgt unmittelbar:
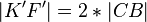
- Aus (2) und (3) folgt unmittelbar:
- Der Spiegel ist also (mindestens) halb so hoch wie die Person.
- Analog kann man herleiten, dass
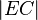 halb so groß ist wie
halb so groß ist wie 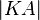 und
und
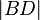 halb so groß ist wie
halb so groß ist wie 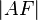 .
.
- Der Spiegel ist also (mindestens) halb so hoch wie die Person.
--EarlHickey (Diskussion) 19:20, 9. Feb. 2014 (CET)
Hallo EarlHickey,
ich kann leider deine Aufgabe nicht prüfen, da ich an einem fremden PC sitze und Java nicht installieren kann. Kannst du mir die Applikation als Photo einstellen oder mir sagen, welche Punkte B und C sind. Ich kann nämlich trotz erahnter Bezeichnung Schritt 1 nicht nachvollziehen. Zum Lösen der Aufgabe braucht man auf jeden Fall beide Strahlensätze. --Tutorin Anne (Diskussion) 13:58, 10. Feb. 2014 (CET)

