Übung 08.12.14
Aus Geometrie-Wiki
Version vom 4. Dezember 2014, 17:09 Uhr von *m.g.* (Diskussion | Beiträge)
Aufgabe III.01
Gegeben seien die Gerade  durch die Geradengleichung
durch die Geradengleichung 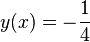 und der Punkt
und der Punkt 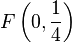 . Beweisen Sie: Für jeden beliebigen Punkt
. Beweisen Sie: Für jeden beliebigen Punkt  auf
auf  gilt: Der Schnittpunkt der Senkrechten
gilt: Der Schnittpunkt der Senkrechten  auf
auf  in
in  mit der Mittelsenkrechten von
mit der Mittelsenkrechten von 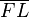 ist ein Punkt der Normalparabel.
ist ein Punkt der Normalparabel.

