Untergruppen SoSe 2017
Aus Geometrie-Wiki
Version vom 14. Mai 2017, 16:50 Uhr von *m.g.* (Diskussion | Beiträge)
UntergruppenBeispiele
DefinitionDefinition 6: (Untergruppe)
Untergruppenkriterium 1Satz 2: (1. Untergruppenkriterium)
Beweis: Übungsaufgabe Untergruppenkriterium 2Satz 3: (2. Untergruppenkriterium)
|
Beweis: Übungsaufgabe
![[\mathbb{Z}|_2, +]](/images/math/b/f/a/bfac4357e3f1dc2a83e6dd4dd6349274.png) ist eine Untergruppe von
ist eine Untergruppe von ![[\mathbb{Z}, +]](/images/math/8/2/8/828d3197747f0dc881f51c684f1a4c7d.png)
![[G,\odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe und
eine Gruppe und 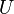 eine Teilmenge von
eine Teilmenge von  .
.![[U,\odot]](/images/math/a/c/c/accc85078e0a1b7e699636b07b93c89b.png) selbst eine Gruppe ist, dann ist
selbst eine Gruppe ist, dann ist 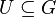 mit
mit 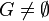 .
.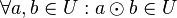 ,
,
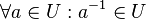 .
.
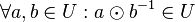 .
.

