Lösung von Aufgabe 4.3 (WS 18 19)
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel  und
und  . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
1. 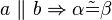
Stufenwinkelsatz--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 21:17, 5. Nov. 2018 (CET)
2. 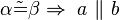
Umkehrung Stufenwinkelsatz--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 21:17, 5. Nov. 2018 (CET)
3. 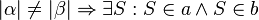
Die Geraden wären identisch was sie laut Aufgabenstellung nicht sein dürfen.--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 21:17, 5. Nov. 2018 (CET)
ok, aber die Frage ist, ob diese Aussage trotzdem äquivalent zum Stufenwinkelsatz ist?--Schnirch (Diskussion) 13:27, 7. Nov. 2018 (CET)
4. 
Äuivalente Aussage--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 21:17, 5. Nov. 2018 (CET)
nun, das ist eine Äquivalenzaussage, aber ist sie auch äquivalent zum Stufenwinkelsatz?--Schnirch (Diskussion) 13:27, 7. Nov. 2018 (CET)

