Lösung von Aufgabe 13.2
Aus Geometrie-Wiki
Version vom 16. Juli 2010, 19:07 Uhr von Löwenzahn (Diskussion | Beiträge)
Satz XII.4: (Innenwinkelsatz für Dreiecke)
- Es sei
 ein Dreieck mit den Innenwinkeln
ein Dreieck mit den Innenwinkeln 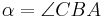 ,
, 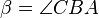 und
und 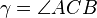 .
.
Es gilt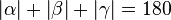 .
.
- Es sei
Versuch 1
VSS: Dreieck  , mit Innenwinkel
, mit Innenwinkel 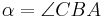 ,
, 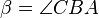 und
und 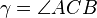
Beh: 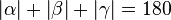
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 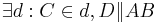
|
(Euklidisches Parallelenaxiom) |
| (II) |  und und 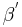 sind Stufenwinkel sind Stufenwinkel
|
(I), (Def. Stufenwinkel) |
| (III) |  und und 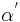 sind Stufenwinkel sind Stufenwinkel
|
(I), (Def. Stufenwinkel) |
| (IV) |  und und 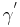 sind Scheitelwinkel sind Scheitelwinkel
|
(I), (Def. Scheitelwinkel) |
| (V) | 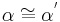 , , 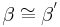
|
(I), (II), (III), (Stufenwinkelsatz) |
| (VI) | 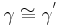
|
(I), (IV), (Scheitelwinkelsatz) |
| (VII) | 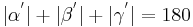
|
(Def. Nebenwinkel), (Supplementaxiom) |
| (VIII) | 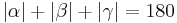
|
(VII), (V), (VI) |
-> Beh. wahr qed
--Löwenzahn 18:07, 16. Jul. 2010 (UTC)

