Lösung von Aufgabe 13.2
Aus Geometrie-Wiki
Version vom 19. Juli 2010, 08:07 Uhr von *m.g.* (Diskussion | Beiträge)
Satz XII.4: (Innenwinkelsatz für Dreiecke)
- Es sei
 ein Dreieck mit den Innenwinkeln
ein Dreieck mit den Innenwinkeln 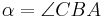 ,
, 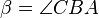 und
und 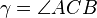 .
.
Es gilt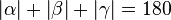 .
.
- Es sei
Versuch 1
VSS: Dreieck  , mit Innenwinkel
, mit Innenwinkel 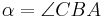 ,
, 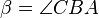 und
und 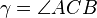
Beh: 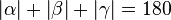
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 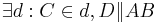
|
(Euklidisches Parallelenaxiom) |
| (II) |  und und 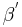 sind Stufenwinkel sind Stufenwinkel
|
(I), (Def. Stufenwinkel) |
| (III) |  und und 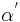 sind Stufenwinkel sind Stufenwinkel
|
(I), (Def. Stufenwinkel) |
| (IV) |  und und 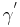 sind Scheitelwinkel sind Scheitelwinkel
|
(I), (Def. Scheitelwinkel) |
| (V) | 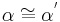 , , 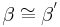
|
(I), (II), (III), (Stufenwinkelsatz) |
| (VI) | 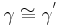
|
(I), (IV), (Scheitelwinkelsatz) |
| (VII) | 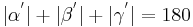
|
(Def. Nebenwinkel), (Supplementaxiom) |
| (VIII) | 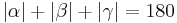
|
(VII), (V), (VI) |
-> Beh. wahr qed
--Löwenzahn 18:07, 16. Jul. 2010 (UTC)
Kommentar --*m.g.* 07:07, 19. Jul. 2010 (UTC): Ich bin mal ganz pingelig. EP sagt aus, dass es durch einen nicht zu  gehörenden Punkt
gehörenden Punkt  höchstens eine Gerade
höchstens eine Gerade  geben kann, die zu
geben kann, die zu  parallel ist. Kann man Schritt (I) wirklich mit EP begründen?
parallel ist. Kann man Schritt (I) wirklich mit EP begründen?

