Lösungen Serie 5 SoSe 2020

Aufgabe 6.02

Anfrage von Ferrus

nun, ich habe mir noch etwas Gedanken gemacht zu meiner Lösung 6.02. Ich bin zum Entschluss gekommen, dass es vielleicht geschickter gewesen wäre, Strecken als Punktmengen zu behandeln, da somit die Definition eindeutiger wäre. Was sagen Sie dazu Herr Gieding? (Änderung 31.05.2020 22:29)

Antwort

Ja, Strecken werden üblicherweise als Punktmengen definiert. Hier die formale Definition: 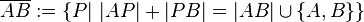$\overline{AB}:=\{P|~|AP|+|PB|=|AB|\cup \{A,B\}\}$.
Was bedeutet diese Definition in "einfachen Worten"?--*m.g.* (Diskussion) 11:27, 3. Jun. 2020 (CEST)

anderer Lösungsvorschlag

a) Die Menge aller Punkte, die zwischen den Punkten A und B liegen, heißt offene Strecke.
b) Die Menge aller Punkte einer offenen Strecke und der Endpunkte A und B heißt geschlossene Strecke.
c) Die Menge aller Punkte einer offenen Strecke und genau einem der beiden Endpunkte A und B heißt halboffene Strecke.
d) Der Abstand der Endpunkte einer Strecke 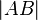$|AB|$ ist die Länge der Strecke $\overline{AB}$.
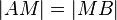e) Der Punkt M einer Strecke $\overline{AB}$, für den $|AM|=|MB|$ gilt, heißt Mittelpunkt der Strecke $\overline{AB}$.
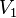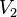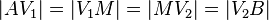f) Die Punkte $V_1$, $M$ und $V_2$ einer Strecke $\overline{AB}$, mit $M$ als Mittelpunkt von $\overline{AB}$, für die $|AV_1|=|V_1M|=|MV_2|=|V_2B|$ gilt, heißen Viertelpunkte der Strecke $\overline{AB}$.

Aufgabe 6.03

[[Datei:

Aufgabe 6.03

]]

Bemerkung

Es handelt sich aus der Sicht der Mathematikdidaktik um eine sogenannte informelle Definition. Schon ein wenig mehr als nur rein intuitiv verstanden, aber aus Sicht des formalen Mathematikers formal nicht ganz korrekt, da etwa der Begriff Richtung noch nicht sauber formuliert wurde. Entweder wir definieren jetzt was eine "Richtung" ist oder versuchen es mit einem anderen bereits definierten Begriff. Da wäre wohl nur "liegt zwischen" im Angebot.
Das "Herantasten" an eine formal korrekte Definition über ein informelle Definition ist wichtig, kennzeichnet dieser Weg doch ein Verständnis für den Begriff. Das Formale ist dann eigentlich "nur" noch Übersetzung.--*m.g.* (Diskussion) 11:40, 3. Jun. 2020 (CEST)

Andere Herangehensweise

Der Begriff der Richtung ist nicht ganz einfach. Der Mathematiker definiert Richtung anders als wir es umgangssprachlich tun würden. Eine Richtung ist in der Mathematik eine Äquivalenzklasse zueinander paralleler Geraden. Das was wir jetzt noch brächten wäre eigentlich der sogenannte Richtungssinn: nach links, nach rechts, nach oben, nach unten. Wir sehen, dass dieser Begriff ein paar Schwierigkeiten mit sich bringt, da man einen Richtungsinn auf einer Geraden irgendwie vor dem anderen auszeichnen müsste.
Es geht aber auch über die Relation "zwischen" ... .--*m.g.* (Diskussion) 11:46, 3. Jun. 2020 (CEST)
Zum Experimentieren: Halbgeraden über die Zwischenrelation:

Aufgabe 6.04

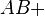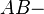Bei der Zerlegung einer Geraden AB in zwei Halbgeraden $AB+$ und $AB-$ ist die Menge aller Punkte zwischen A und B sowie die Punkte A und B in beiden Halbgeraden und in diesem Fall in beiden Teilmengen enthalten. Somit gilt Bedingung (III) nicht, welche besagt dass jedes Element nur in einer Teilmenge enthalten sein darf. Da nicht alle drei Bedingungen erfüllt sind, liegt keine Klasseneinteilung vor.

Aufgabe 6.05

Reicht das?

Es gibt ja nur noch eine weitere Möglichkeit. Streng genommen müssen Sie diese Möglichkeit im Beweis berücksichtigen. Es ist aber abzusehen, dass in diesem beweis nur ein paar Punktbezeichnungen anders sind. Also verweisen wir auf den Fall und sagen "Beweis analog".--*m.g.* (Diskussion) 11:34, 3. Jun. 2020 (CEST)

Aufgabe 6.06

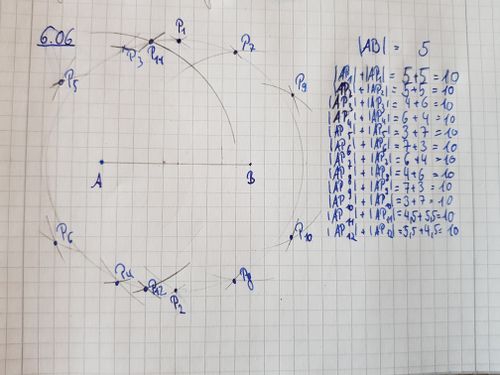
Sieht gut aus. --*m.g.* (Diskussion) 12:08, 3. Jun. 2020 (CEST)

Hier eine Variante mit Geogebra: Ellipse mit zwei Kreisen in Geogebra

Aufgabe 6.07 und 6.08

anderer Lösungsvorschlag

6.07

Für C ist Element von 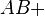$AB+$ kann zw(A,B,C) oder zw(A,C,B) gelten. Da |AB|<|AC| kann |AC|+|CB|=|AB| nicht gelten, weil |CB| nicht negativ sein kann (Axiom II.1). zw(A,C,B) kann folglich nicht gelten. Da von drei paarweise verschiedenen kollinearen Punkten immer genau einer zwischen den anderen beiden liegt, muss zw(A,B,C) gelten.

6.08

Voraussetzung: Die Geraden g und h haben genau einen Schnittpunkt.
Behauptung: Die Geraden sind komplanar.
Beweis:
(1) Es existiert der Schnittpunkt S der beiden Geraden g und h. (V)
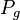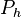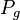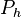(2) Es existieren die Punkte $P_g$, der mit g inzidiert, und $P_h$, der mit h inzidiert. $P_g$ und $P_h$ sind verschieden von S.(Axiom I.2)
(3) Es gilt 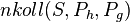$nkoll(S,P_h,P_g)$ (V)
(4) Es existiert eine Ebene E, die diese drei Punkte enthällt. (1, 2, 3, Axiom I.4)
(5) Die Geraden g und h sind in der Ebene E enthalten (4, Axiom I.5)

(6) g und h sind komplanar (5)[[Datei:

Aufgabe 6.07

]]