Aufgaben zur Vorbereitung auf die Klausur
Inhaltsverzeichnis |
Aufgabe 14.1
Es sei  ein Dreieck.
ein Dreieck. 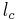 sei die Lotgerade des Lotes von
sei die Lotgerade des Lotes von  auf
auf  .
. 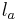 sei die Lotgerade des Lotes von
sei die Lotgerade des Lotes von  auf
auf 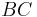 und
und 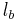 sei die Lotgerade des Lotes von
sei die Lotgerade des Lotes von  auf
auf 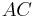 . Man beweise:
. Man beweise: 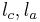 und
und 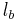 haben genau einen Punkt gemeinsam.
haben genau einen Punkt gemeinsam.
Aufgabe 14.2
Es sei  ein Punkt aus dem Inneren des Winkels
ein Punkt aus dem Inneren des Winkels  . Man beweise:
. Man beweise:  ist genau dann ein Punkt der Winkelhalbierenden
ist genau dann ein Punkt der Winkelhalbierenden 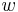 von
von  , wenn er zu den Schenkeln von
, wenn er zu den Schenkeln von  jeweils ein und denselben Abstand hat.
jeweils ein und denselben Abstand hat.
Aufgabe 14.3
Das Euklidische Parallelenaxiom findet man in einigen Lehrbüchern in der folgenden Formulierung: Zu jedem Punkt  außerhalb einer Geraden
außerhalb einer Geraden  gibt es genau eine Gerade
gibt es genau eine Gerade  mit
mit 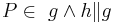 . Warum genügt diese Formulierung des Euklidischen Parallelenaxioms nicht den Anforderungen, die an Axiome zu stellen sind?
. Warum genügt diese Formulierung des Euklidischen Parallelenaxioms nicht den Anforderungen, die an Axiome zu stellen sind?
Aufgabe 14.4
Der Begriff des Drachen sei wie folgt definiert: Unter einem Drachen versteht man ein konvexes Viereck mit zwei Paaren benachbarter Seiten, die kongruent zueinander sind.
Man beweise: Wenn ein Viereck  ein Drachen ist, dann halbiert eine Diagonale dieses Vierecks die andere Diagonale von
ein Drachen ist, dann halbiert eine Diagonale dieses Vierecks die andere Diagonale von  .
.

