Satz des Pythagoras WS 23 24
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
1. Wiederholung Satz des Thales
Bewege den Punkt C, der auf dem Kreis entlangläuft, indem du mit der linken Maustaste draufdrückst, die Taste gedrückt hältst und die Maus bewegst. Was kannst du beobachten? Was verändert sich? Besprich deine Beobachtungen mit deinem:deiner Sitznachbarin.
Beobachte nun den Winkel α. Verändert sich seine Größe, wenn du den Punkt C bewegst?
Vervollständige nun den Satz des Thales:
Ein Dreieck, dessen drei Punkte A, B und C auf einem _______________ liegen, und dessen Strecke AB der ______________ des Dreiecks ist, ist immer ein __________________ Dreieck.
2. Hinführung Satz des Pythagoras
Das Dreieck, dass du eben schon in der Aufgabe zum Satz des Thales untersucht hast, wurde nun mit den drei Flächen 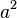 ,
, 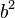 und c12 ergänzt. Die Flächen wurden aus dem Quadrat der jeweiligen Seiten gebildet (z.B. Seite a: a*a = a2 = Fläche). Die Flächen sind deshalb quadratisch.
Bewege nun erneut den Punkt C und beobachte, wie sich die Flächen a2, b2 und c12 verändern. Besprich dich mit deinem:deiner Sitznachbar:in. Haltet eure Beobachtungen schriftlich fest, indem ihr die folgenden Sätze mit „wahr“ oder „falsch“ bewertet.
und c12 ergänzt. Die Flächen wurden aus dem Quadrat der jeweiligen Seiten gebildet (z.B. Seite a: a*a = a2 = Fläche). Die Flächen sind deshalb quadratisch.
Bewege nun erneut den Punkt C und beobachte, wie sich die Flächen a2, b2 und c12 verändern. Besprich dich mit deinem:deiner Sitznachbar:in. Haltet eure Beobachtungen schriftlich fest, indem ihr die folgenden Sätze mit „wahr“ oder „falsch“ bewertet.

