Aufgabe 1 Lösungsversuch
Wir haben zu zeigen, dass 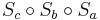 =
= 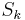
Es genügt zu zeigen, dass eine Gerade k existiert, die gleichzeitig Mittelsenkrechte von 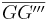 ,
, 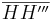 und
und 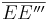 ist.
ist.
Wir wissen, dass alle drei Mittelsenkrechten der drei Strecken 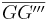 ,
, 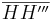 und
und 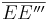 den Punkt Z gemeinsam haben (wegen der Abstandserhaltung und des Mittelsenkrechtenkriteriums)
den Punkt Z gemeinsam haben (wegen der Abstandserhaltung und des Mittelsenkrechtenkriteriums)
Wenn wir nun noch zeigen können, dass sie einen weiteren Punkt gemeinsam haben, dann haben wir gezeigt, dass die drei Mittelsenkrechten identisch sind und damit, dass die Spiegelung von 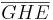 das Dreieck auf
das Dreieck auf 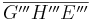 abbildet und wären damit fertig.
abbildet und wären damit fertig.
Wir ezigen nun, dass der Punkt L1 neben der Mittelsenkrechte von 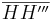 noch auf den anderen beiden Mittelsenkrechten liegt:
noch auf den anderen beiden Mittelsenkrechten liegt:
| Beweisschritt | Begründung |
|---|---|
1) Das Dreieck 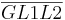 ist kongruent zu dem Dreieck ist kongruent zu dem Dreieck 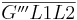
|
SWS (kann sich, denke ich, jeder selbst überlegen) |
2) 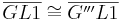
|
(1) |
3) L1 liegt auch auf der Mittelsenkrechten von 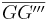
|
(2) |
4) Analog kann man zeigen, dass L1 auch auf der Mittelsenkrechten von 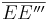 liegt. liegt.
|
|
5) Damit sind die drei Mittelsenkrechten von 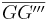 , , 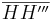 und und 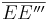 identisch und damit ist gezeigt, dass identisch und damit ist gezeigt, dass 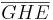 bei der Spiegelung an k auf bei der Spiegelung an k auf 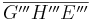 abgebildet wird. abgebildet wird.
|
Der Beweis ist nur ein Versuch. Wäre schön wenn jemand (am besten herr Gieding ;)) mal drüberschauen würde. --Steph85

