Lösung von Aufg. 11.3

Beweisen Sie Satz VII.6 a:

Wenn ein Punkt $\ P$ zu den Endpunkten der Strecke $\overline{AB}$ jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von $\overline{AB}$ .

--------------------------------------------------------------------

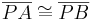
Voraussetzung:Es sei eine Strecke $\overline{AB}$ und ein Punkt P mit $\overline{PA} \cong \overline{PB}$

Behauptung: 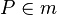$P \in m$ , m ist Mittelsenkrechte von $\overline{AB}$

Fall 1: koll(A,B,P)
Fall 2: nkoll(A,B,P)

Beweis zu Fall 1
Nr.	Beweisschritt	Begründung
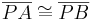(I)	P ist Mittelpunkt von $\overline{AB}$	Vor.( $\overline{PA} \cong \overline{PB}$ ),Def.III.1 (Mittelpunkt)
(II)	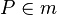$P \in m$	I, Def VI.1(Mittelsenkrechte)

Beweis zu Fall 2
Nr.	Beweisschritt	Begründung
(I)	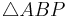$\triangle ABP$ ist gleichschenklig	Vor.(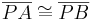 $\overline{PA} \cong \overline{PB}$ ), Def.VII.4 (gleichschenkliges Dreieck)
(II)	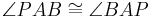$\angle PAB \cong \angle BAP$	I, Satz VII.5 (Basiswinkelsatz)
(III)	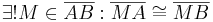$\exists ! M \in \overline{AB} : \overline{MA} \cong \overline{MB}$	Satz III.1(Existenz und Eindeutigkeit des Mittelpunkts), Def.III.1 (Mittelpunkt)
(IV)	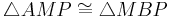$\triangle AMP \cong \triangle MBP$	II, III, Vor.(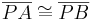 $\overline{PA} \cong \overline{PB}$ ), Axiom V (SWS)
(V)	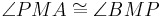$\angle PMA \cong \angle BMP$	IV, Def.VII.3 (Dreieckskongruenz)
(VI)	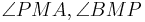$\angle PMA , \angle BMP$ sind Nebenwinkel	IV, Def.V.4 (Nebenwinkel)
(VII)	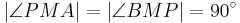$\| \angle PMA \| = \| \angle BMP \| = 90^{\circ}$	V, VI, Def V.6 (rechter Winkel)
(VIII)	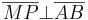$\overline{MP} \bot \overline{AB}$	VII, Def.V.9 (noch mehr Senkrecht)
(IX)	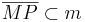$\overline{MP} \subset m$	III, VIII, Def.VI.1 (Mittelsenkrechte)
(X)	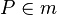$P \in m$	IX