Lösung von Aufg. 12.1
Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Voraussetzung: Dreieck ABC,  ,
,  ,
,  .
.
Behauptung: mindestens zwei Innenwinkel sind spitz
Annahme: zwei Innenwinkel sind nicht spitz o.B.d.A  und
und  .
.
Beweisschritt (Begründung)
1.  >90 und
>90 und  >90 (Annahme)
>90 (Annahme)
2.  ist Außenwinkel (Definition Außenwinkel)
ist Außenwinkel (Definition Außenwinkel)
3.  +
+  =180 (Supplementaxiom)
=180 (Supplementaxiom)
4.  <90 (1,3 rechnen in R)
<90 (1,3 rechnen in R)
5.  <
<  . (1,4)
. (1,4)
Widerspruch zum schwachen Außenwinkelsatz, Annahme ist zu verwerfen Behauptung stimmt
--Sommer80 16:05, 19. Jan. 2011 (UTC)
Schritt 1. sollte man durch "größergleich" 90 ergänzen, sonst ist der Beweis nicht korrekt, denn die Winkel könnten ja genau 90 sein und wären dann auch nicht spitz.--Tutorin Anne 09:07, 27. Jan. 2011 (UTC)
weiterer Lösungsvorschlag:
Vor: Dreieck ABC,  >90
>90
Beh: <90,
<90, <90
<90
1)  >90_____________________Vor.
>90_____________________Vor.
2) 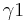 <90_________________
<90_________________ 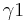 ist Nebenwinkel von
ist Nebenwinkel von 
3) 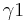 ist Außenwinkel des Dreiecks ABC___________________schwacher Außenwinkelsatz und 2)
ist Außenwinkel des Dreiecks ABC___________________schwacher Außenwinkelsatz und 2)
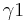 >90
>90 
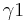 >90
>90 
4) <
<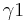 <90_________________________2) und 3)
<90_________________________2) und 3)
 <
<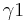 <90
<90
5) und
und  sind spitze Winkel________________4)--Engel82 11:05, 22. Jan. 2011 (UTC)
sind spitze Winkel________________4)--Engel82 11:05, 22. Jan. 2011 (UTC)
Der Beweis lässt sich so ähnlich auch direkt durchführen, allerdings stimmen die Begründungen nicht immer. bei 2) Begründung zu Ergänzen mit Supplementaxiom bei 3) steht die Begründung im Beweisschritt; besser ist es, den Schritt wegzulassen und Schritt 4) dann mit dem schwachen Außenwinkelsatz und 2) zu begründen. Auch hier muss größergleich (hier =<) verwendet werden, damit der Fall=90 nicht ausgeschlossen ist. z.B.: 1)
>=90_____________________Vor.
2)=<90_________________
ist Nebenwinkel von
; Supplementaxiom
3)<
=<90
<
=<90_________________________2) und
ist Außenwinkel des Dreiecks ABC
; schwacher Außenwinkelsatz 5)und
sind spitze Winkel________________3)Def. spitze Winkel--Tutorin Anne 09:07, 27. Jan. 2011 (UTC)

