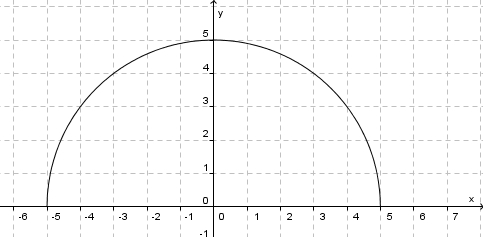
Definition der Woche 7 (SoSe 11)

Definieren Sie den Begriff "Halbkreis".
Sei k ein Kreis (bzw. die Menge aller Punkte, die von einem Punkt M ein und den selben Abstand haben) und Strecke d eine Kreissehne für die gilt: Mittelpunkt M ist Element d.
Die Menge aller Punkte, die von M ein und den selben Abstand haben und Unterhalb der Sehne d liegen, heißt Halbkreis.

Man könnte jetzt natürlich annehmen: "Was ist mit den ganzen Punkten, die Oberhalb der Sehen liegen." Aber aufgrund der Invarianz denke ich dass es soweit keine Rolle spielt.

Definition Kreis:
Sei k ein Kreis (s.o) mit dem Mittelpunk M und dem Durchmesser d.
Sei X Element von k und X kein Element von d.
H := {y Element von k | XY(Strich oben drüber) geschnitten d ={} }

H heißt Halbkreis.
Je nach Wahl von X ergeben sich zwei verschiedene Halbkreise
--Peterpummel 20:23, 17. Mai 2011 (CEST)
Hallo Peterpummel,
das musst du bitte kurz erklären. ich hab das was du beschrieben hast mal nach bestem Wissen und Gewissen im Geogebra generiert und siehe da - alles andere als ein Halbkreis.

ich denke um einen Halbkreis zu generieren, ist es entscheident, im Zentrum des Kreises, also im Mittelpunkt anzufangen, wenn du auf dem Kreis, aus dem dein Halbkreis entstehen soll einen Punkt legst und daran arbeitest gehst du fehl.

sollte ich mich jedoch wahnsinnig geirrt haben, dann gerne eine verbesserung. --Flo60 22:57, 17. Mai 2011 (CEST)