Lösung von Aufg. 12.3 SS11

Beweisen Sie Satz VII.6 a:

Wenn ein Punkt $\ P$ zu den Endpunkten der Strecke $\overline{AB}$ jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von $\overline{AB}$.

$\ Beweis:$

$\ V: \overline{AP} \equiv \overline{BP}$
$\ B: \ P\in \ m \ mit \ m \ ist \ Mittelsenkrechte \ von \ \overline{AB}$

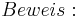
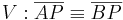
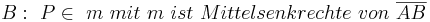
Skizze dazu: (--Tutorin Anne 17:33, 5. Jul. 2011 (CEST))

$\ Sei \ M \ Mittelpunkt \ von \ \overline{AB}\ ( \ n. \ Existenz \ vom \ Mittelpunkt \ einer \ Strecke)$
$\ Betrachte \ die \ beiden \ Dreieck \ \overline{AMP}\ und\ \overline{MPB}$
$\ Es \ gilt \ : \ \overline{AP} \equiv \overline{BP}\ nach \ Voraussetzung\$
$\ Ferner\ \angle PMA \equiv \angle PBM \ nach \ Basiswinkelsatz$
$\ und \ \overline{AM} \equiv \overline{MB} \ da \ M \ Mittelpunkt\ ist.$
$\Rightarrow \ nach \ SWS \ die \ Kongruenz \ der \ beiden \ Dreiecke$
$\Rightarrow \angle PMA\equiv \angle BMP\Rightarrow \ es \ sind \ rechte \ Winkel \Rightarrow \ PM \ ist \ Mittelsenkrechte$
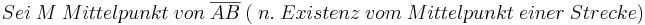
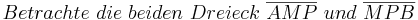
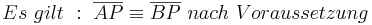
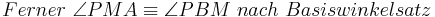
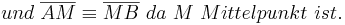
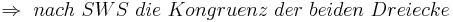
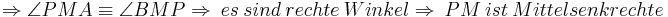
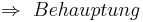$\Rightarrow \ Behauptung$--Peterpummel 17:47, 3. Jul. 2011 (CEST)

Der Beweis ist gut, allerdings solltest du wie Phil den 2. Fall nicht vergessen, denn dann ergäben sich ja keine Dreiecke.--Tutorin Anne 17:33, 5. Jul. 2011 (CEST)

Lösungsvorschlag 2:

$\ Vor: \ Punkt \ P, \ Strecke \overline{AB}, \ Mittelsenkrechte \ m \ von \overline{AB}$
$|\ PA | = | \ PB |$
$\ Beh: \ P \in \ m$

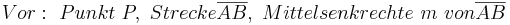
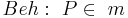
Man muss in zwei Fälle unterscheiden:
$\ 1. \ Fall: \ P \neq \ M$
$\ 2. \ Fall: \ P \ = \ M$

$\ 1. Fall: \ P \neq \ M$
$\ 1) \triangle \overline{ABP} \ ist \ gleichschenklig \ (Vor, \ Def. \ gleichschenkliges \triangle \ )$
$\ 2) \exists \ Winkelhalbierende \ w \ des \angle \ APB \ (Existenz \ und \ Eindeutigkeit \ der \ Winkelhalbierenden)$
$\ 3) \ w \ teilt \angle \ APB \ in \ y1 \ und \ y2, \ y1 \ = \ y2 \ (Def. \ Winkelhalbierende)$
$\ 4) \ w \cap \overline{AB} \ = \ P2 \ (Lemma1)$
$\ 5)|\ PA | = | \ PB | \ (Vor.)$
$\ 6) \ y1 \ = \ y2 \ (3)$
$\ 7) \angle \ PAB \cong \angle \ PBA \ (1, \ Basiswinkelsatz)$
$\ 8) \triangle \ APP2 \cong \triangle \ BPP2 \ (WSW, \ 5, \ 6, \ 7)$
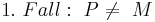
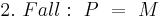
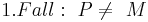
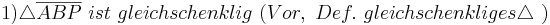
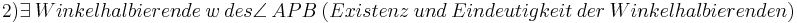
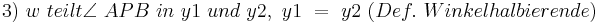
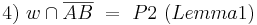
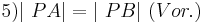
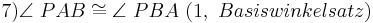
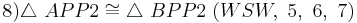
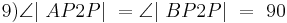$\ 9) \angle | \ AP2P | \ = \angle | \ BP2P | \ = \ 90$ (8, Def. Nebenwinkel, Supplementaxiom)
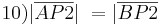$\ 10) | \overline{AP2} | \ = | \overline{BP2}$ (8)
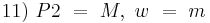$\ 11) \ P2 \ = \ M, \ w \ = \ m$ (10, Def. Mittelpunkt, 9, Def. Mittelsenkrechte)
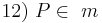$\ 12) \ P \in \ m$ (9, 10, 11)

$\ 2. \ Fall: \ P \ = \ M$
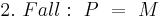
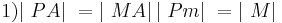$\ 1) | \ PA | \ = | \ MA | \, | \ Pm | \ = | \ M |$ (Annahme 2. Fall)
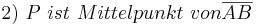$\ 2) \ P \ ist \ Mittelpunkt \ von \overline{AB}$ (Def. Mittelpunkt, 1)
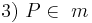$\ 3) \ P \in \ m$ (2, Def. Mittelsenkrechte)---phil- 15:04, 5. Jul. 2011 (CEST)