Lösung von Aufg. 12.9 SS11
Aus Geometrie-Wiki
Version vom 7. Juli 2011, 15:01 Uhr von WikiNutzer (Diskussion | Beiträge)
Es seien  ein gleichseitiges Dreieck und
ein gleichseitiges Dreieck und  eine positive reelle Zahl, die kleiner als die Seitenlänge von
eine positive reelle Zahl, die kleiner als die Seitenlänge von  ist. Ferner seien die Punkte
ist. Ferner seien die Punkte 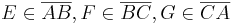 mit
mit 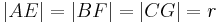 gegeben. Man beweise:
gegeben. Man beweise: 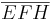 ist ein gleichseitiges Dreieck.
ist ein gleichseitiges Dreieck.
Auch hier wäre die Definition des gleichseitigen Dreiecks gefragt.
--Peterpummel 15:55, 4. Jul. 2011 (CEST)
Das stimmt, diese brauch man zunächst! Wer hat Vorschläge?--Tutorin Anne 18:32, 5. Jul. 2011 (CEST)
Wenn ein Dreieck drei kongruente Seiten hat, ist es gleichseitig.
Dann liefe der Beweis analgog zu Aufgabe 12.8, allerdings müsste man nichts mehr über die Innenwinkel des kleinen Dreiecks in der Mitte aussagen, da hier ja nur die Seiten maßgeblich wären:
Richtig?--WikiNutzer 16:01, 7. Jul. 2011 (CEST)

