Lösung von Aufg. 12.3 SS11
Beweisen Sie Satz VII.6 a:
- Wenn ein Punkt
 zu den Endpunkten der Strecke
zu den Endpunkten der Strecke  jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von  .
.
- Wenn ein Punkt
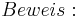
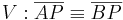
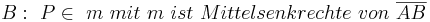
Skizze dazu: (--Tutorin Anne 17:33, 5. Jul. 2011 (CEST))
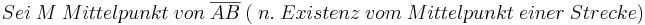
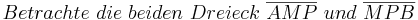
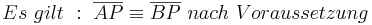
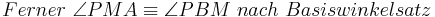 (davor sollte man noch sagen, das hier ein gleichschenkliges Dreieck vorliegt > wo sollen sonst Basiswinkel vorliegen?)
(davor sollte man noch sagen, das hier ein gleichschenkliges Dreieck vorliegt > wo sollen sonst Basiswinkel vorliegen?)
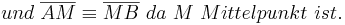
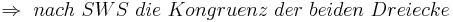
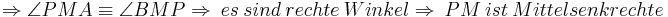
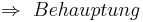 --Peterpummel 17:47, 3. Jul. 2011 (CEST)
--Peterpummel 17:47, 3. Jul. 2011 (CEST)
Der Beweis ist gut, allerdings solltest du wie Phil den 2. Fall nicht vergessen, denn dann ergeben sich ja keine Dreiecke.--Tutorin Anne 17:33, 5. Jul. 2011 (CEST)
Lösungsvorschlag 2:
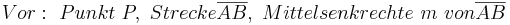

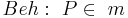
Man muss in zwei Fälle unterscheiden:
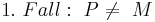
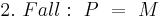
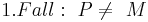
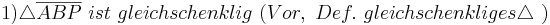
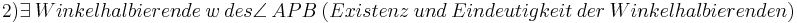
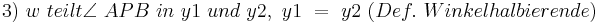
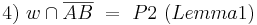
5)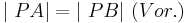
6) 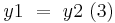 Nicht einfach Schritte oder Vorausetzung wiederholen!
Nicht einfach Schritte oder Vorausetzung wiederholen!
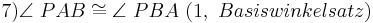
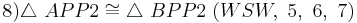
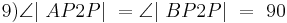 (8, Def. Nebenwinkel, Supplementaxiom)
(8, Def. Nebenwinkel, Supplementaxiom)
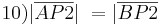 (8)
(8)
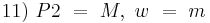 (10, Def. Mittelpunkt, 9, Def. Mittelsenkrechte)
(10, Def. Mittelpunkt, 9, Def. Mittelsenkrechte)
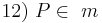 (9, 10, 11)
(9, 10, 11)
Ich denke, auch so kann Fall I beweisen werden. Scheint mir aufwendiger, aber auch richtig. Gut!--Tutorin Anne 17:57, 5. Jul. 2011 (CEST)
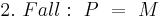
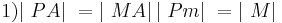 (Annahme 2. Fall) (Hier verstehe ich nicht, was du damit zeigen willst. --Tutorin Anne 17:57, 5. Jul. 2011 (CEST))
(Annahme 2. Fall) (Hier verstehe ich nicht, was du damit zeigen willst. --Tutorin Anne 17:57, 5. Jul. 2011 (CEST))
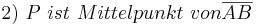 (Def. Mittelpunkt, 1)
(Def. Mittelpunkt, 1)
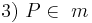 (2, Def. Mittelsenkrechte)---phil- 15:04, 5. Jul. 2011 (CEST)
(2, Def. Mittelsenkrechte)---phil- 15:04, 5. Jul. 2011 (CEST)

