Lösung von Aufg. 12.9 SS11
Es seien  ein gleichseitiges Dreieck und
ein gleichseitiges Dreieck und  eine positive reelle Zahl, die kleiner als die Seitenlänge von
eine positive reelle Zahl, die kleiner als die Seitenlänge von  ist. Ferner seien die Punkte
ist. Ferner seien die Punkte 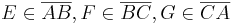 mit
mit 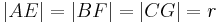 gegeben. Man beweise:
gegeben. Man beweise: 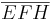 ist ein gleichseitiges Dreieck.
ist ein gleichseitiges Dreieck.
Auch hier wäre die Definition des gleichseitigen Dreiecks gefragt.
--Peterpummel 15:55, 4. Jul. 2011 (CEST)
Das stimmt, diese brauch man zunächst! Wer hat Vorschläge?--Tutorin Anne 18:32, 5. Jul. 2011 (CEST)
Wenn ein Dreieck drei kongruente Seiten hat, ist es gleichseitig.
Dann liefe der Beweis analgog zu Aufgabe 12.8, allerdings müsste man nichts mehr über die Innenwinkel des kleinen Dreiecks in der Mitte aussagen, da hier ja nur die Seiten maßgeblich wären: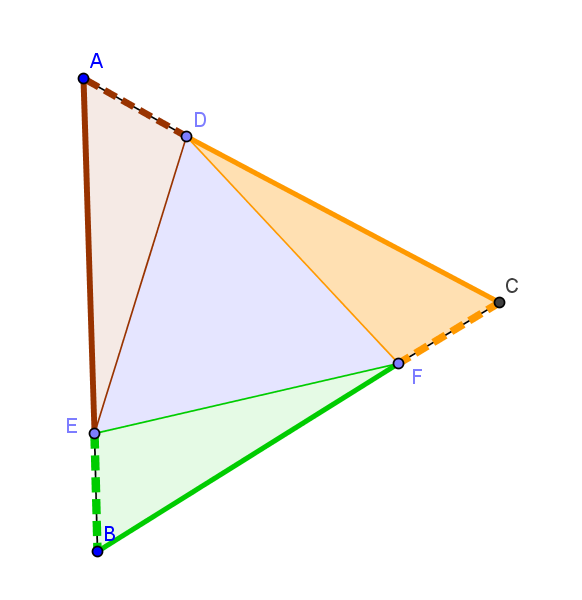
1. Aus der Voraussetzung wissen wir, dass die gestrichelten Strecken gleich lang sind (nämlich jeweils r), außerdem, dass die Außenseiten des großen Dreiecks auch gleich lang sind.
2. Aus dem Streckenaddieren und den Voraussetzungen wissen wir damit, dass auch die dicken durchgehenden Strecken gleich lang sind.
3. Aus den Voraussetzungen und (z.B.) dem Basiswinkelsatz wissen wir außerdem, dass die Innenwinkel des großen Dreiecks alle gleich groß sind.
4. Da nun das grüne, das rote und das gelbe Dreieck per SWS-Axiom als kongruent nachgewiesen werden, müssen auch die Außenseiten des blauen Dreiecks alle gleich lang sein.
5. Und wenn ein gleichseitiges Dreieck einfach über die drei gleichlangen Seiten definiert ist, ist der Beweis damit geführt.
Richtig?--WikiNutzer 16:01, 7. Jul. 2011 (CEST)
Ich denke, ja! Sehr anschaulicher Beweis mit der Skizze, danke!--Tutorin Anne 16:42, 8. Jul. 2011 (CEST)
Ja, so habe ich es auch - nur dass in der Voraussetzung die dicken Strecken als kongruent ausgewiesen sind, nicht die gestrichelten - aber dann kannst du ja analog vorgehen.--mm_l 11:02, 15. Jul. 2011 (CEST) Statt Streckenaddieren würde ich die Def. Zwischenrelation nehmen, da hierbei immer 2 Komponenten gleich groß sind, muss auch die 3. Teilstrecke gleich groß sein?--mm_l 11:12, 15. Jul. 2011 (CEST)

